1/3等于0.333（除不尽），那么1米长的绳子能否分成三等份？
这种问题经常在网络上出现，很容易让人陷入某种误区，甚至让人患上“强迫症”，看到无理数就会产生某种说不清道不明的“歧视”心理，就好像无理数真的“无理”一样，“无理数”这三个字确实蒙蔽了很多人的双眼！
事实上无理数一点也不“无理”，无理数和有理数完全是平等的，都是一个再普通不过的数，而且是真实存在的数，一个非常确定的数。
无理数与有理数的区别只有一点：无限不循环，仅此而已。
但你不能因为无限不循环就对无理数“另眼看待”，甚至会下意识地认为“无限不循环就不是确定的数”！
不少人总是下意识习惯性地强迫无理数必须用小数完全写出来，写不出来心里就憋得慌。但一个非常现实的问题是：为何一定要用小数写出来呢？用其他形式写出来不行吗？
这就是不少人认识山的误区！
比如说圆周率π就是π，就好比“1就是1”一样，都是一个确定的数。我可以很轻松地把π写出来，它就是：π。
明白了这点，再回到问题中。
1/3等于0.333......，永远写不完，但写不完不代表1/3就不存在，事实上你可以非常轻松地在数周上画出1/3长度，不但如此，你可以在数周上画出任何一个数（包括无理数）的长度，比如说π，√2等。
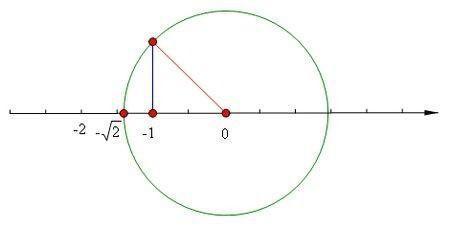
下图一眼就能看出如何在数轴上画出√2：画一个直角边为1的等腰直角三角形，然后以斜边为半径画一个圆形，与数轴的交点就是√2。
确实，在人类数学史上，尤其是在微积分思想产生之前，无理数的概念困惑了很多人。就好题目中的问题一样，0.333永远写不完，怎么可能分成三等份呢？
首先1/3是一个确定的数，非常确定，是一个实数。只要是实数，都会对应数轴上的一个点。我们经常用到的圆周率π是无理数，它也对应数轴上一个点，π是一个确定的长度。
不少人认为无理数是不那么确定的数，其实只是一种错觉，一种心理暗示罢了，或者说是一种“强迫症”！
肯定有人会这样质问：1米长的绳子分成三等份，一份的长度就是0.333......，那么三份的长度应该是0.999......，也不等于1啊！
这就是误区所在，其中也牵扯到极限的思想。
最简单的解释就是：不要总是在0.333......（一直循环）上面较真，你直接认为1/3不就行了吗？1/3乘以3不正好等于1吗？为什么非要把任何数都要写成小数的形式才甘心呢？
但总会有人不甘心，一定要用小数写出来才罢休。所以问题的关键就在于：0.999......是否等于1？
0.999......等于1，0.999......等于1，0.999......等于1。
重要的事情说三遍！
可以用反证法来证明，首先假设0.999......不等于1，由于两个不相等的数之间肯定会存在无数多个数，这意味着0.999......和1之间存在无数多个数，但事实上不要说找到无数多个数了，你能找到哪怕一个数吗？
如果能找到，0.999......当然不等于1，如果找不到，0.999......必然等于1。最后的结果是：你不得不承认0.999......等于1。虽然你可能还是那么不甘心！
还有人经常会这样问：0.999......不是比1要小0.00000......1吗？极限属于一种抽象概念，非具体的，所以我们不能用具体数值的加减来理解。
再举个通俗的例子。
自然数与偶数哪个更多？
如果没有极限的思想概念，很容易得出“自然数比偶数多”的结论，毕竟自然数包括偶数和奇数。但事实上自然数与偶数一样多。自然数与偶数都是无穷多个，无穷也是有大小的。最简单的比较无穷大小的方式就是两个无穷的合集是否能一一对应。
自然数虽然看起来比偶数多（好像多出来的都是奇数），但每一个自然数都有偶数与之对应：自然数乘以2不就是偶数吗？
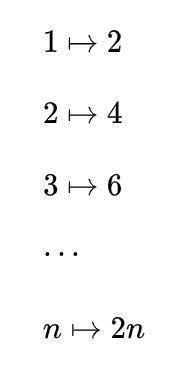
所以自然数与偶数一样多！
如果你按照刚才的思想来较真：自然数-偶数=奇数，那就完全脱离了极限的思想。
最后还要强调一点，从理论上分析，一根一米长的绳子可以分成三等份，但现实中你永远做不到。这与科技发达与否没有关系，科技再发达也不可能做到，误差是永远存在的。
而且“一根一米长的绳子分成三等份”仅仅是从数学概念来分析的，也就是说数轴上长度为1的线段可以分成三等份。但数学并不等同于现实，数学可以说是抽象的概念，带有绝对性。而测量属于具体的，具有相对性。
同时，数学上不存在最小的数，你永远找不到大于0的最小的数，但现实中存在最小的长度单位，它就是普朗克长度，任何小于普朗克长度的单位都没有意义！
最新文章
-
张秀东注释
4小时前 -
北宋这些县到了金朝，为何出现治所大搬家的情况，发生了什么事
4小时前 -
黑神话悟空：看懂金蝉子为啥被贬，才明白黄眉为什么要祸乱人间
5小时前 -
RSI选股方法
5小时前 -
古玉图谱 – 书格
5小时前 -
西藏和青海是如何纳入中国版图的来看吐蕃瓦解后千年历史演变
5小时前 -
炒股秘籍，实图讲解MACD指标，零轴金叉技巧选出买点！
5小时前 -
请你欣赏宋代名画------晴春蝶戏图
5小时前
有话要说...