经典的分形算法

小宇宙

被誉为大自然的几何学的分形（）理论，是现代数学的一个新分支，但其本质却是一种新的世界观和方法论。它与动力系统的混沌理论交叉结合，相辅相成。它承认世界的局部可能在一定条件下，在某一方面（形态，结构，信息，功能，时间，能量等）表现出与整体的相似性，它承认空间维数的变化既可以是离散的也可以是连续的，因而拓展了视野。

分形几何的概念是美籍法国数学家曼德布罗（B.B.）1975年首先提出的，但最早的工作可追朔到1875年，德国数学家维尔斯特拉斯（K.）构造了处处连续但处处不可微的函数，集合论创始人康托（G.，德国数学家）构造了有许多奇异性质的三分康托集。1890年，意大利数学家皮亚诺（G.Peano）构造了填充空间的曲线。1904年，瑞典数学家科赫（H.von Koch）设计出类似雪花和岛屿边缘的一类曲线。1915年，波兰数学家谢尔宾斯基（W.）设计了象地毯和海绵一样的几何图形。这些都是为解决分析与拓朴学中的问题而提出的反例，但它们正是分形几何思想的源泉。1910年，德国数学家豪斯道夫（F.）开始了奇异集合性质与量的研究，提出分数维概念。1928年布利干（G.）将闵可夫斯基容度应用于非整数维，由此能将螺线作很好的分类。1932年庞特里亚金（L.S.）等引入盒维数。1934年，贝塞考维奇（A.S.）更深刻地提示了豪斯道夫测度的性质和奇异集的分数维，他在豪斯道夫测度及其几何的研究领域中作出了主要贡献，从而产生了豪斯道夫-贝塞考维奇维数概念。以后，这一领域的研究工作没有引起更多人的注意，先驱们的工作只是作为分析与拓扑学教科书中的反例而流传开来。

真正令大众了解分形是从计算机的普及肇始，而一开始，分形图的计算机绘制也只是停留在二维平面，但这也足以使人们心驰神往。近来，一个分形体爱好者丹尼尔·怀特（英国一钢琴教师）提出一个大胆的方法，创造出令人称奇的3D分形影像，并将它们命名为芒德球（）。

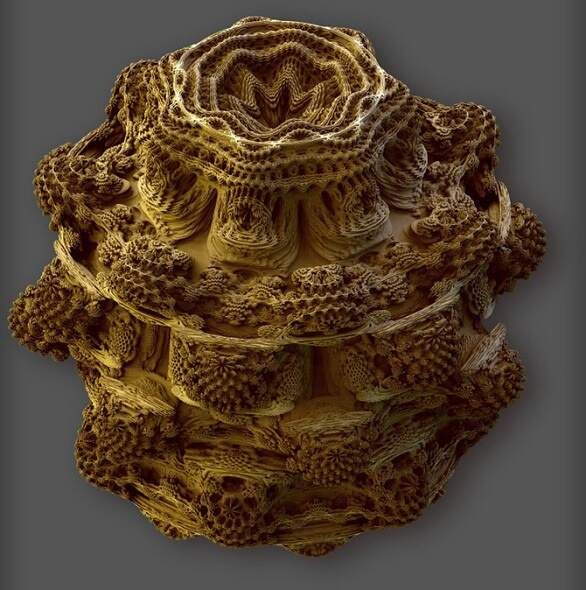
在芒德球极其繁琐的外表下，这个集合实际上是由一种非常基础的算法得出的。那是一种利用复数的算法。就曼德布罗集而言，它是直接由最简单的乘方运算得出的——对复数进行乘方。但问题在于无法在三维空间恰当地扩展数的概念。与复数和平面点之间的关系不同，19世纪的数学家们曾证明，立体空间中的点是无法用适宜传统加法和乘法运算的代数工具来表示的。既然无法定义数字计算，自然也就无法勾画曼德布罗集的三维形象。解决方案之一是在四维空间中进行计算，然后将结果投射到三维空间中。四维空间中的每个点都可与 “四元数”（）匹配，对它们可以进行传统算术操作。尽管四维空间无法用肉眼看到，但利用四元数便能轻而易举地列出与曼德布罗集相对应的算法，之后去掉一个分量，就能使结果显示成三维效果。但这个方案也令人失望，得到的画面比二维图像好不了多少。

为了避开这个难题，丹尼尔·怀特两年前冒出一个古怪的想法。彻底摆脱数学的羁绊，他在三维空间的点与点之间凭空构建出一种“伪分形”。尽管其处理手段算不上中规中矩的乘法，但至少将与曼德布罗集相对应的算法扩展到了三维空间中所有的点。丹尼尔·怀特对几百万个点进行了计算，之后又追加了光影和纹理以体现立体效果，终于，在他的屏幕上呈现出第一个芒德球，形状与严格的曼德布罗集十分近似。遗憾的是，这一结果没能满足他的期望：“图形令人惊叹，但我期望的是更精致的细节。”

尝试并未就此止步。丹尼尔·怀特在互联网上的一个分形体论坛上引起了美国一位年轻计算机专家保罗·尼兰德的注意。他接手怀特的研究，对算法进行稍事改动，把反复的平方操作换成更高次方（八次方），从而得到了一系列新的芒德球，指数越高，细节就越丰富。

这个芒德球引起了我的极大兴趣，下决心要学学分形体，于是乎决定从最简单的分形算法学起，希望与各位共勉。

以下开始介绍几例最简单的分形算法：

一、三分集的递归算法

选取一个欧氏长度的直线段，将该线段三等分，去掉中间一段，剩下两段。将剩下的两段分别再三等分，各去掉中间一段，剩下四段。将这样的操作继续下去，直到无穷，则可得到一个离散的点集。点数趋于无穷多，而欧氏长度趋于零。经无限操作，达到极限时所得到的离散点集称之为集。

1.给定初始直线两个端点的坐标（ax，ay）和（bx，by），按三分集的生成规则计算出个关键点的坐标如下：

cx=ax+(bx-ax)/3

cy=ay-d

dx=bx-(bx-ax)/3

dy=by-d

ay=ay-d

by=by-d

2.利用递归算法，将计算出来的新点分别对应于（ax，ay）和（bx，by），然后利用步骤1的计算关系计算出下一级新点（cx，cy）和（dx，dy），并压入堆栈。

3.给定一个小量c，当（bx，by）下面给出程序：

f=(ax,ay,bx,by)

c=0.005;d=0.005;

if (bx-ax)>c

x=[ax,bx];y=[ay,by];hold on;

plot(x,y,'',2);hold off;

cx=ax+(bx-ax)/3;

cy=ay-d;

dx=bx-(bx-ax)/3;

dy=by-d;

ay=ay-d;

by=by-d;

(ax,ay,cx,cy);

(dx,dy,bx,by);

end

运行（0,5,5,5），出现图例如下：

二、Koch曲线的递归算法

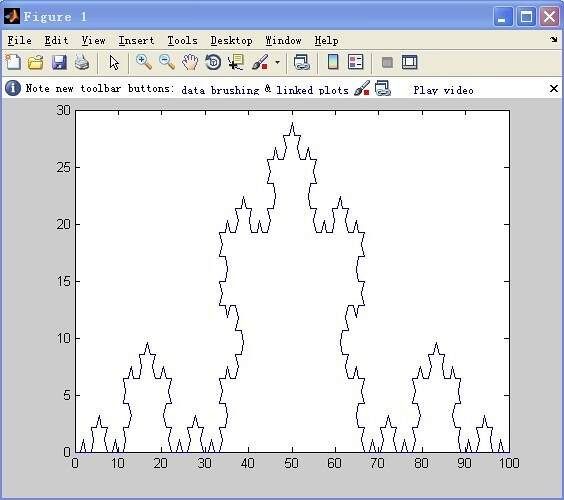
在一单位长度的线段上对其三等分，将中间段直线换成一个去掉底边的等边三角形，再在每条直线上重复以上操作，如此进行下去直到无穷，就得到分形曲线Koch曲线。

1.给定初始直线（ax，ay）-（bx，by），按Koch曲线的构成原理计算出各关键点坐标如下：

cx=ax+(bx-ax)/3

cy=ay+(by-ay)/3

ex=bx-(bx-ax)/3

ey=by-(by-ay)/3

l=sqrt((ex-cx)^2+(ey-cy)^2)

alpha=atan((ey-cy)/(ex-cx))

dy=cy+sin(alpha+pi/3)*l

dx=cx+cos(alpha+pi/3)*l

2.利用递归算法，将计算出来的新点分别对应于（ax，ay）和（bx，by），然后利用步骤1中的计算公式计算出下一级新点（cx，cy），（dx，dy），（ex，ey），并压入堆栈。

3.给定一个小量c，当l下面给出程序：

f=Koch(ax,ay,bx,by,c)

if (bx-ax)^2+(by-ay)^2x=[ax,bx];y=[ay,by];

plot(x,y);hold on;

else

cx=ax+(bx-ax)/3; cy=ay+(by-ay)/3;

ex=bx-(bx-ax)/3; ey=by-(by-ay)/3;

l=sqrt((ex-cx)^2+(ey-cy)^2);

alpha=atan((ey-cy)/(ex-cx));

if (alpha>=0&(ex-cx)alpha=alpha+pi;

end

dy=cy+sin(alpha+pi/3)*l;

dx=cx+cos(alpha+pi/3)*l;

Koch(ax,ay,cx,cy,c);

Koch(ex,ey,bx,by,c);

Koch(cx,cy,dx,dy,c);

Koch(dx,dy,ex,ey,c);

end

运行Koch(0,0,100,0,10)，出现图例如下：

三、生成填充Julia集

1.设定参数a，b以及一个最大的迭代步数N。

2.设定一个限界值R，即实数R≧max（2，sqrt（a^2+b^2）。

3.对于平面上以R为半径的圆盘内的每一点进行迭代，如果对于所有的n≦N，都有|x^2+y^2|≦R，那么，在屏幕上绘制出相应的起始点，否则不绘制。

下面给出程序：

a=-0.11;b=0.65;r=2;

for x0=-1:0.01:1

for y0=-1:0.01:1

x=x0;y=y0;

if x0^2+y0^2for n=1:80

x1=x*x-y*y+a;

y1=2*x*y+b;

x=x1;

y=y1;

end

if (x*x+y*y)plot(x0,y0);

end

hold on;

end

end

end

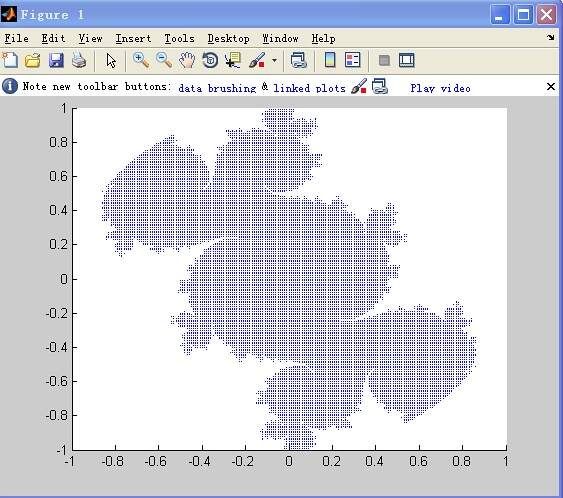
a=-0.11,b=0.65

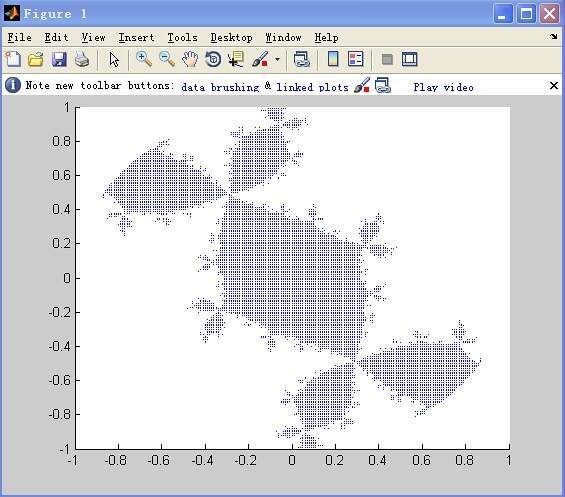
a=-0.13,b=0.77

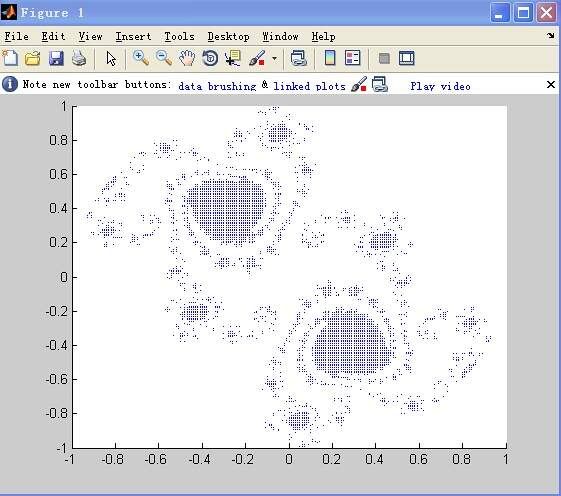
a=-0.19,b=0.6557

四、牛顿迭代

牛顿迭代是在数值求解非线性方程（组）的时候经常使用的方法。有些牛顿迭代能够绘制出漂亮的图形来，所以现在也常用于设计图形。

程序如下：

首先编写函数：

y=(z)

if (z==0)

y=0;

;

end

for i=1:1:2000

y=z-(z^3-1)/(3*z^2);

if (abs(y-z)break;

end

z=y;

end

接着进入主程序：

clear all;clc;

A=1;B=0;C=1;

for a=-1:0.005:1

for b=-1:0.005:1

x0=a+b*i;

y=(x0);

if abs(y-A)plot(a,b,'r');hold on;

abs(y-B)plot(a,b,'g');hold on;

abs(y-C)plot(a,b,'y');hold on;

end

end

end

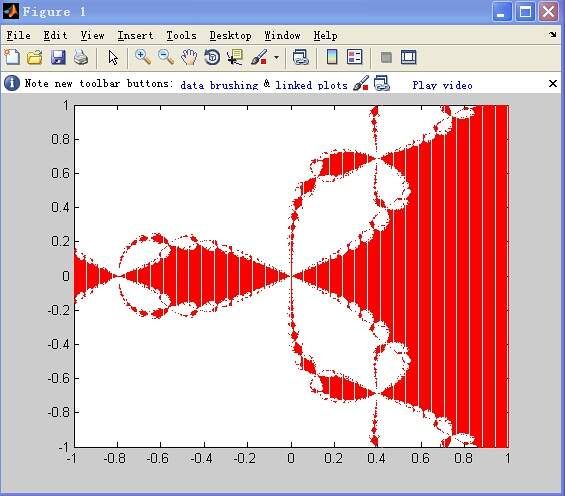
五、迭代函数系IFS

IFS是分形的重要分支。它是分形图像处理中最富生命力而且最具有广阔应用前景的领域之一。这一工作最早可以追溯到于1981年对自相似集的研究。美国科学家M.F.于1985年发展了这一分形构型系统，并命名为迭代函数系统（ ，IFS），后来又由 Demko等人将其公式化，并引入到图像合成领域中。IFS将待生成的图像看做是由许多与整体相似的（自相似）或经过一定变换与整体相似的（自仿射）小块拼贴而成。

算法：

1.设定一个起始点（x0，y0）及总的迭代步数。

2.以概率P选取仿射变换W，形式为

X1=a x0+b y0 +e

Y1=c x0+d y0+f

3.以W作用点（x0，y0），得到新坐标（x1，y1）。

4.令x0=x1，y0=y1。

5.在屏幕上打出（x0，y0）。

6.重返第2步，进行下一次迭代，直到迭代次数大于总步数为止。

下面给出一些IFS植物形态的程序：

a=[0.195 -0.488 0.344 0.433 0.4431 0.2452 0.25;

0.462 0.414 -0.252 0.361 0.2511 0.5692 0.25;

-0.058 -0.07 0.453 -0.111 0.5976 0.0969 0.25;

-0.035 0.07 -0.469 -0.022 0.4884 0.5069 0.2;

-0.637 0 0 0.501 0.8562 0.2513 0.05];

x0=1;y0=1;

for i=1:10000

r=rand;

if r0.25 & r0.5 & r0.75 & r0.95 & r0;

[p,r,n,a]=(p,r/2,n-1,a+pi/3,C);

n=n+1;r=r*2;a=a-pi/3;

[zr(1),r,n,a]=(zr(1),r/4,n-1,a,C);

n=n+1;r=r*4;

[zr(2),r,n,a]=(zr(2),r/4,n-1,a,C);

n=n+1;r=r*4;

[zr(3),r,n,a]=(zr(3),r/4,n-1,a,C);

n=n+1;r=r*4;

end

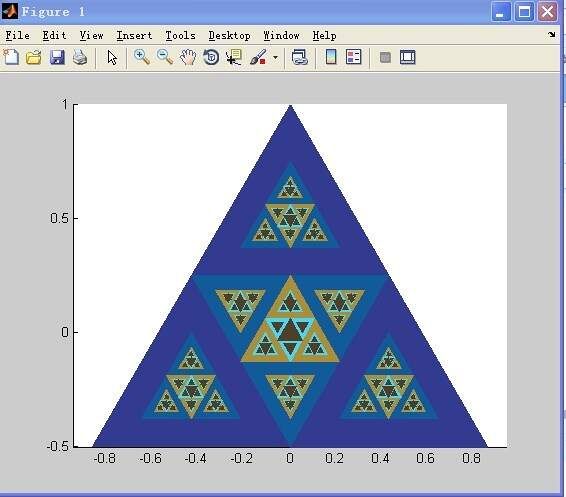
大家觉得这是否和一些教堂玻璃艺术很相近呢？有的数学家甚至说艺术就是分形。

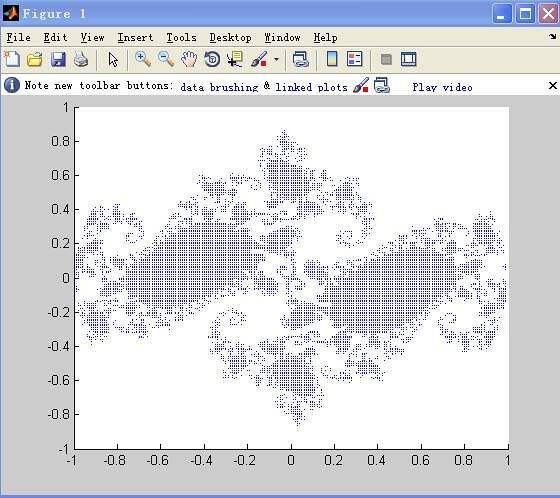
七、曼德布罗集合

set是在复平面上组成分形的点的集合。集合可以用复二次多项式f(z)=z^2+c来定义。其中c是一个复参数。对于每一个c，从z=0开始对f(z)进行迭代序列 (0, f(0), f(f(0)), f(f(f(0))), .......)的值或者延伸到无限大，或者只停留在有限半径的圆盘内。曼德布罗集合就是使以上序列不延伸至无限大的所有c点的集合。从数学上来讲，曼德布罗集合是一个复数的集合。一个给定的复数c或者属于曼德布罗集合M，或者不是。

1.设定参数a，b，以及一个最大的迭代步数N。

2.设定一个限界值R，不妨设实数R=2。

3.对于参数平面上的每一点c（a，b），使用以R为半径的圆盘内的每一点进行迭代，如果对于所有的n≤N，都有|x*x+y*y|≤R*R，那么，在屏幕上绘制出相应的起始点c（a，b），否则不绘制。

下面给出程序：

r=4;%限界值

for a=-2:0.002:1

for b=-2:0.002:1%参数a，b取到一个范围

x=a;y=b;%初始的复数c

for n=1:20

x1=x*x-y*y+a;%复数平方加一个c的运算

y1=2*x*y+b;

x=x1;%迭代

y=y1;

end

if(x*x+y*y)plot(a,b);

end

hold on;

end

end

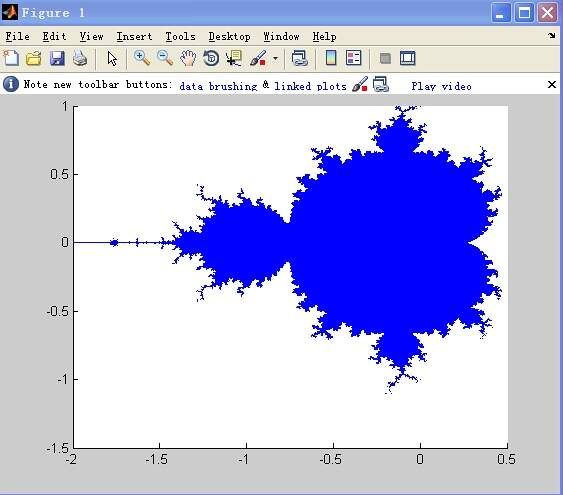
八、脑分形

作为IFS的一种应用

a=[0.03 0 0 0.45 0 0 0.05;

-0.03 0 0 -0.45 0 0.4 0.15;

0.56 -0.56 0.56 0.56 0 0.4 0.4;

0.56 0.56 -0.56 0.56 0 0.4 0.4];

x0=1;y0=1;

for i=1:

r=rand;

if r0.05 & r0.2 & r0.6 & r