小学奥数题型与解题思路21~40讲

21、数字和与最大最小问题

　　【数字求和】

　　例1 100个连续自然数的和是8450，取其中第1个，第3个，第5个，………，第99个（所有第奇数个），再把这50个数相加，和是______。

　　（上海市第五届小学数学竞赛试题）

　　讲析：第50、51两个数的平均数是8450÷ 100= 84. 5，所以，第50个数是84。则100个连续自然数是：

　　35，36，37，………，133，134。

　　上面的一列数分别取第1、3、5、……、99个数得：

　　35，37，39，……131，133。

　　则这50个数的和是：

　　

　　例2 把1至100的一百个自然数全部写出来，所用到的所有数码的和是_____。

　　（上海市第五届小学数学竞赛试题）

　　讲析；可把1至100这一百个自然数分组，得

　　（1、2、3、……、9），（10、11、12、……、19），（20、21、22、……29），……，（90、91、92、……99），（100）。

　　容易发现前面10组中，每组的个位数字之和为45。而第一组十位上是0，第二组十位上是1，第三组十位上是2，……第十组十位上是9，所以全体十位上的数字和是（l+2+3+……+9）×10=450。故所有数码的和是45×10+450+l=901。

　　

续若干个数字之和是1992，那么a=____。

　　（北京市第八届“迎春杯”小学数学竞赛试题）

　　

　　又，1992÷27=73余21，而21=8+5+7+1，所以a=6。

　　例4 有四个数，每次选取其中三个数，算出它们的平均数，再加上另外一个数，用这种方法计算了四次，分别得到四个数：86，92，100，106。那么，原来四个数的平均数是

　　（1993年全国小学数学奥林匹克决赛试题）

　　讲析：每次所选的三个数，计算其平均数，实际上就是计算这三个数中

原来四个数的平均数为（86+92+100+106）÷2=192。

　　【最大数与最小数】

　　例1 三个不同的最简真分数的分子都是质数，分母都是小于20的合数，要使这三个分数的和尽可能大,这三个分数是

　　（全国第四届《从小爱数学》邀请赛试题）。

　　讲析： 20以内的质数有： 2、 3、 5、 7、 11、 13、 17、 19

　　要使三个分数尽量大，必须使每个分子尽量大而分母尽量小。且三个真

　　例2 将1、2、3、4、5、6、7、8这八个数分成三组，分别计算各组数的和。已知这三个和互不相等，且最大的和是最小和的2倍。问：最小的和是多少？

　　（全国第三届“华杯赛”决赛口试试题）

　　讲析；因为1+2+3+……+8=36，又知三组数的和各不相同，而且最大的

　　例3 把20以内的质数分别填入□中（每个质数只用一次）：

　　

　　使A是整数。A最大是多少？

　　（第五届《从小爱数学》邀请赛试题）

　　讲析：要使A最大，必须使分母尽量小，而分子尽量大。

　　分母分别取2、3、5时，A都不能为整数。当分母取7时，

　　

　　例4 一组互不相同的自然数，其中最小的数是1，最大的数是25。除1之外、这组数中的任一个数或者等于这组数中某一个数的2倍，或者等于这组数中某两个数之和。问：这组数之和的最大值是多少？当这组数之和有最小值时，这组数都有哪些数？并说明和是最小值的理由。

　　（全国第四届“华杯赛”决赛第一试试题）

　　 析：观察自然数1、2、3、4、5、……、25这25个数，发现它们除1之外，每个数都能用其中某一个数的2倍，或者某两个数之和表示。因此，这组数之和的最大值是1+2+3+……+25=325。

　　下面考虑数组中各数之和的最小值。

　　1和25是必取的，25不能表示成一个数的2倍，而表示成两个数之和的形式，共有12种。我们取两个加数中含有尽可能大的公约数的一组数（20+5）或者（10+15）。当取1、5、20、25时，还需取2、3、10三个；当取1、10、15、25时，还需取2、3、5。经比较这两组数，可知当取1、2、3、4、5、10、15、25时，和最小是61。

22、数字串问题

　　【找规律填数】

　　例1 找规律填数

　　

　　（杭州市上城区小学数学竞赛试题）

　　　　

　　（1992年武汉市小学数学竞赛试题）

　　讲析：数列填数问题，关键是要找出规律；即找出数与数之间有什么联系。

　　第（1）小题各数的排列规律是:第1、3、5、……（奇数）个数分别

别是4和2。

　　第（2）小题粗看起来，各数之间好像没有什么联系。于是，运用分数

得到了　

　　

　　

　　例2 右表中每竖行的三个数都是按照一定的规律排列的。按照这个规律在空格中填上合适的数。

　　（1994年天津市小学数学竞赛试题）

　　讲析：根据题意，可找出每竖行的三个数之间的关系。不难发现每竖行中的第三个数，是由前两数相乘再加上1得来的。所以空格中应填33。

　　【数列的有关问题】

　　　

数是几分之几？

　　（第一届《从小爱数学》邀请赛试题）

　　讲析：经观察发现，分母是1、2、3、4、5……的分数个数，分别是1、3、5、7、9……。所以，分母分别为1、2、3……9的分数共

　

　　　

　　

　　例2 有一串数：1，1993，1992，1，1991，1990，1，1989，1988，…这个数列的第1993个数是______

　　（首届《现代小学数学》邀请赛试题）

　　讲析：把这串数按每三个数分为一组，则每组第一个数都是1，第二、三个数是从1993开始，依次减1排列。

　　而1993÷3=664余1，可知第1993个数是1。

　　例3 已知小数0.12345678910111213……9899的小数点后面的数字，是由自然数1—99依次排列而成的。则小数点后面第88位上的数字是______。

　　（1988年上海市小学数学竞赛试题）

　　讲析：将原小数的小数部分分成A、B两组：

　　

　　A中有9个数字，B中有180个数字，从10到49共有80个数字。所以，第88位上是4。

　　例4 观察右面的数表（横排为行，竖排为列）；

　　　

　　

几行，自左向右的第几列。（全国第三届“华杯赛”决赛试题）

　　讲析：第一行每个分数的分子与分母之和为2，第二行每个分数的分子与分母之和为3，第三行每个分数的分子与分母之和为4，……即每行各数的分子与分母之和等于行数加1。

　　　

　　例5 如图5.4，除了每行两端的数之外，其余每个数都是与它相连的上一行的两个数的平均数，那么第100行各数之和是_______。

　　（广州市小学数学竞赛试题）

　　讲析：可试探着计算每行中各数之和。第一、二、三、四行每行的各数之和分别是6、8、10、12，从而得出，每行的数字之和，是行数的2倍加4。故第100行各数之和为100×2＋4=204.

　　例6 伸出你的左手，从大拇指开始，如图5.5所示的那样数数：l、2、3……。问：数到1991时，会落在哪个手指上？

　　（全国第三届“华杯赛”决赛口试试题）

　　讲析：除1之外，从2开始每8个数为一组，每组第一个数都是从食指开始到拇指结束。∵（1991—1）÷8=248余6，∴剩下最后6个数又从食指开始数，会到中指结束。

　　例7 如图5.6，自然数按从小到大的顺序排成螺旋形。在“2”处拐第一个弯，在“3”处拐第二个弯……问拐第二十个弯处是哪个数？

　　（全国第一届“华杯赛”决赛口试试题）

　　讲析：写出拐弯处的数，然后按每两个数分为一组：（2，3），（5，7），（10，13），（17，21），（26，31），……。将会发现，每组数中依次相差1、2、3、4、5、……。每组的第二个数与后一组的第二个数依次相差2、3、4、5、……。从而可推出，拐第二十个弯处的数是111。

　　例8 自然数按图5.7顺次 排列。数字3排在第二行第一列。问：1993排在第几行第几列？

　　（全国第四届“华杯赛”复赛试题）

　　讲析：观察每斜行数的排列规律，每斜行数的个数及方向。

　　每一斜行数的个数分别是1、2、3、4、5、……，奇数斜行中的数由下向上排列，偶数斜行中的数由上向下排列。

　　

斜行，该斜行的数是由下向上排列的，且第63行第1列是1954。

　　由于从1954开始，每增加1时，行数就减少1，而列数就增加1。所以1993的列数、行数分别是：

　　1993—1954＋1=40（列），63-（1993—1954）=24（行）

23、数阵图

　　【方阵】

　　例1 将自然数1至9，分别填在图5.17的方格中，使得每行、每列以及两条对角线上的三个数之和都相等。

　　（长沙地区小学数学竞赛试题）

　　讲析：中间一格所填的数，在计算时共算了4次，所以可先填中间一格的数。

　　（l+2+3+……+9）÷3=15，则符合要求的每三数之和为15。显然，中间一数填“5”。

　　再将其它数字顺次填入，然后作对角线交换，再通过旋转（如图5.18），便得解答如下。

　　例2 从1至13这十三个数中挑出十二个数，填到图5.19的小方格中，使每一横行四个数之和相等，使每一竖列三个数之和又相等。

　　（“新苗杯”小学数学竞赛试题）

　　讲析：据题意，所选的十二个数之和必须既能被 3整除，又能被 4整除，（三行四列）。所以，能被12整除。十三个数之和为91，91除以12，商7余7，因此，应去掉7。每列为（91—7）÷4=21

　　而1至13中，除7之外，共有六个奇数，它们的分布如图5.20所示。

　　三个奇数和为21的有两种：21=1＋9+11=3＋5+13。经检验，三个奇数为3、5、13的不合要求，故不难得出答案，如图5.21所示。

　　例3 十个连续自然数中，9是第三大的数，把这十个数填到图5.22的十个方格中，每格填一个，要求图中三个2×2的正方形中四数之和相等。那么，这个和数的最小值是______。

　　（1992年全国小学数学奥林匹克初赛试题）

　　讲析：不难得出十个数为:2、3、4、5、6、7、8、9、10、11。它们的和是65。在三个2×2的正方形中，中间两个小正方形分别重复了两次。

　　设中间两个小正方形分别填上a和b，则（65＋a＋b）之和必须是 3的倍数。所以，（a＋b）之和至少是7。

　　故，和数的最小值是24。

　　【其他数阵】

　　例1 如图5.23，横、竖各12个方格，每个方格都有一个数。

　　已知横行上任意三个相邻数之和为20，竖列上任意三个相邻数之和为21。图中已填入3、5、8和“×”四个数，那么“×”代表的数是______。

　　（1994年全国小学数学奥林匹克初赛试题）

　　讲析：可先看竖格。因为每相邻三格数字和为21，所以每隔两格必出现重复数字。从而容易推出，竖格各数从上而下是：3、10、8、3、10、8、3、10、8、3、10、8。

　　同理可推导出横格各数，其中“×”=5。

　　例2 如图5.24，有五个圆，它们相交后相互分成九个区域，现在两个区域里已经分别填上数字10、6，请在另外七个区域里分别填进2、3、4、5、6、7、9七个数字，使每个圆内的数之和都是15。

　　（上海市第五届小学数学竞赛试题）　

　　讲析：可把图中要填的数，分别用a、b、c、d、e、f、g代替。（如图5.25）

　　显然a=5，g=9。

　　则有：b＋c=10，e＋f=6，c＋d＋e=15。经适当试验，可得b=3，c=7，d=6，e=2，f=4。

　　例3 如图5.26，将六个圆圈中分别填上六个质数，它们的和是20，而且每个小三角形三个顶点上的数之和相等。那么，这六个质数的积是______。

　　（全国第一届“华杯赛”决赛试题）

　　讲析：最上面的小三角形与中间的小三角形，都有两个共同的顶点，且每个小三角形顶点上三数之和相等。所以，最上边圆圈内数字与最下面中间圆圈内数字相等。

　　同样，左下角与右边中间的数相等，右下角与左边中间数相等。

　　20÷2=10，10＝2+3+5。

　　所以，六个质数积为2×2×3×3×5×5=900。

　　例4 在图5.27的七个○中各填上一个数，要求每条直线上的三个数中，中间一个数是两边两个数的平均数。现已填好两个数，那么X=_______。

　　（1992年全国小学数学奥林匹克决赛试题）

　　讲析：如图5.28，可将圆圈内所填各数分别用a、b、c、d代替。

　　则d=15。

　　由15+c+a=17+c+b，得：a比b多2。

　　所以，b=13+2=15。进而容易算出，x=19。

　　例5 图5.29中8个顶点处标注的数字：

　　a、b、c、d、e、f、g、h，其中的每一个数都等于相邻三个顶点

　

　　（全国第三届“华杯赛”复赛试题）

　　讲析：将外层的四个数，分别用含其它字母的式子表示，得

　　　　

　　　

　　

　　即（a+b+c+d）-（e+f+g+h）=0

24、数的组成

　　【数字组数】

　　例1 用1、2、3、4、5、6、7、8、9这九个数字组成质数，如果每个数字都要用到，并且只能用一次，那么这九个数字最多能组成______个质数。

　　（1990年全国小学数学奥林匹克决赛试题）

　　讲析：自然数1至9这九个数字中，2、3、5、7本身就是质数。于是只剩下1、4、6、8、9五个数字，它们可组成一个两位质数和一个三位质数：41和689。所以，最多能组成六个质数。

　　例2 用0、1、2、……9这十个数字组成五个两位数，每个数字只用一次，要求它们的和是一个奇数，并且尽可能的大。那么，这五个两位数的和是______。

　　（1991年全国小学数学奥林匹克决赛试题）

　　讲析：组成的五个两位数，要求和尽可能大，则必须使每个数尽可能大。所以它们的十位上分别　是9、8、7、6、5，个位上分别是0、1、2、3、4。但要求五个两位数和为奇数，而1+2+3+4=10为偶数，所以应将4与5交换，使和为：

　　（9+8+7+6+4）×10+（1+2+3+5）=351。

　　351即本题答案。

　　例3 一个三位数，如果它的每一个数字都不超过另一个三位数对应数位上的数字，那么就称它被另一个三位数“吃掉”。例如，241被342吃掉，123被123吃掉（任何数都可以被与它相同的数吃掉），但240和223互不被吃掉。现请你设计出6个三位数，它们当中任何一个数不被其它5个数吃掉，并且它们的百位上数字只允许取1、2；十位上数字只允许取1、2、3；个位上数字只允许取1、2、3、4。

　　这6个三位数是_______。

　　（第五届《从小爱数学》邀请赛试题）

　　讲析：六个三位数中，任取两个数a和b，则同数位上的数字中，a中至少有一个数字大于b，而b中至少有一个数字大于a。

　　当百位上为1时，十位上可从1开始依次增加1，而个位上从4开始依次减少1。即：114，123，132。当百位上为2时，十位上从1开始依次增加1而个位上只能从3开始依次减少1。即：213，222，231。经检验，这六个数符合要求。

　　例4 将1、1、2、2、3、3、4、4这八个数字排成一个八位数，使得两个1之间有一个数字；两个2之间有两个数字；两个3之间有三个数字；两个4之间有四个数字。那么这样的八位数中的一个是______。

　　（1991年全国小学数学奥林匹克初赛试题）

　　讲析：两个4之间有四个数字，则在两个4之间必有一个数字重复，而又要求两个1之间有一个数，于是可推知，这个重复数字必定是1，即412134或421314。然后可添上另一个2和3。

　　经调试，得23421314，此数即为所答。

　　【条件数字问题】

　　例1 某商品的编号是一个三位数，现有五个三位数：874，765，123，364，925。其中每一个数与商品编号，恰好在同一位上有一个相同的数字，那么这个三位数是_______

　　（1993年全国小学数学奥林匹克决赛试题）

　　讲析：将五个数按百位、十位、个位上的数字分组比较，可发现：百位上五个数字都不同；十位上有两个2和两个6；个位上有两个4和两个5。故所求的数的个位数字一定是4或5，百位上一定是2或6。经观察比较，可知724符合要求。

　　例2 给一本书编页码，共用了1500个数字，其中数字“3”共用了_______个

　　（首届《现代小学数学）》邀请赛试题）

　　讲析：可先求出1500个数字可编多少页。

　　从第一页到第9页，共用去9个数字；从第10页到第99页，共用去2×90=180（个）数字；余下的数字可编（1500-189）÷3=437（页）

　　所以，这本书共有536页。

　　l至99页，共用20个“3”，从100至199页共用20个“3”，从200至299页共用20个“3”，从300至399页共用去120个“3”，从400至499页共用去20个“3”，从500到536页共用去11个“3”。所以，共用去211个数字3。

　　例3 在三位数中，数字和是5的倍数的数共有_______个。

　　（全国第四届“华杯赛”决赛口试试题）

　　讲析：可把三位数100至999共900个数，从100起，每10个数分为一组，得

　　（100，101、……109），（110、111、……119），……（990、991、……、999）

　　共分成了90组，而每组中有且只有两个数的数字和是5的倍数，所以一共有2×90=180（个）。

　　例4 有四个数，取其中的每两个数相加，可以得到六个和。这六个和中最小的四个数是83、87、92、94，原因数中最小的是______。

　　（上海市第五届小学数学竞赛试题）

　　讲析：设原四个数从小到大为a、b、c、d，则有a+b=83，a+c=87，所以c比b大4。而对于和为92和94时，或者是b+c=92，或者是b+c=94。

　　当b+c=92时，因c比b大4，可得b=45，进而可求得a=38。

　　当b+c=94时，因c比b大4，可得b=44，进而可求得a=39。

　　所以，原四数中最小的数是38或39。

　　

abcd=______

　　（广州市小学数学竞赛试题）

　　讲析：原四位数增加8倍后得新的四位数，也就是原四位数乘以9，得新四位数（如图5.29）。从而可知，a一定为1，否则积不能得四位数。则

　

　　例6 有两个两位数，它们的个位数字相同，十位数字之和是11。这两个数的积的十位数字肯定不会是哪两个数字？

　　（1990年《小学生报》小学数学竞赛试题）

　　讲析：由题意可知，两个数的十位上为（2，9），（3，8），（4，7），（5，6），而个上则可以是0至9的任意一个数字。如果分别去求这两个数的积，那是很麻烦的。

　　设这两个数的个位数字是c，十位数字分别为a、b，则a+b=11，两数分别为（10a+c)，（10b+c）。

　　

　　

字。

　　　　

能是6、8。

　　例7 期的记法是用6个数字，前两个数字表示年份，中间两个数字表示月份，后两个数字表示日（如1976年4月5日记为760405）。

　　第二届小学“祖杯赛”的竞赛日期记为921129。这个数恰好左右对称。因此这样的日期是“吉祥日”。问：从87年9月1日到93年6月30日，共有_______个吉祥日。（第二届“祖冲之杯”小学数学竞赛试题）

　　讲析：一个六位数从中间分开，要求左右对称，则在表示月份的两个数中，只有11月份。而且“年份”的个位数字只能是0、1、2。

　　所以是共有3个吉祥日：901109、911119、921129。

25、数的整除性规律

　　【能被2或5整除的数的特征】（见小学数学课本，此处略）

　　【能被3或9整除的数的特征】一个数，当且仅当它的各个数位上的数字之和能被3和9整除时，这个数便能被3或9整除。

　　例如，1248621各位上的数字之和是

　　1+2+4+8+6+2+1=24

　　3｜24，则3｜1248621。

　　又如，372681各位上的数字之和是

　　3+7+2+6+8+1=27

　　9｜27，则9｜372681。

　　【能被4或25整除的数的特征】一个数，当且仅当它的末两位数能被4或25整除时，这个数便能被4或25整除。

　　例如，173824的末两位数为24，4｜24，则4｜173824。

　　43586775的末两位数为75，25｜75，则25｜

　　43586775。

【能被8或125整除的数的特征】一个数，当且仅当它的末三位数字为0，或者末三位数能被8或125整除时，这个数便能被8或125整除。

　　例如，32178000的末三位数字为0，则这个数能被8整除，也能够被125整除。

　　3569824的末三位数为824，8｜824，则8｜3569824。

　　214813750的末三位数为750，125｜750，则125｜214813750。

【能被7、11、13整除的数的特征】一个数，当且仅当它的末三位数字所表示的数，与末三位以前的数字所表示的数的差（大减小的差）能被7、11、13整除时，这个数就能被7、11、13整除。

　　例如，75523的末三位数为523，末三位以前的数字所表示的数是75，523-75=448，448÷7=64，即

　　7｜448，则7｜75523。

　　又如，1095874的末三位数为874，末三位以前的数字所表示的数是1095，1095-874=221，221÷13=17，即

　　13｜221，则13｜1095874。

　　再如，868967的末三位数为967，末三位以前的数字所表示的数是868，967-868=99，99÷11=9，即

　　11｜99，则11｜868967。

　　此外，能被11整除的数的特征，还可以这样叙述：

　　一个数，当且仅当它的奇数位上数字之和，与偶数位上数字之和的差（大减小）能被11整除时，则这个数便能被11整除。

　　例如，4239235的奇数位上的数字之和为

　　4+3+2+5=14，

　　偶数位上数字之和为2+9+3=14，

　　二者之差为14-14=0，0÷11=0，

　　即11｜0，则11｜4239235。

26、数的公理、定理或性质

　　【小数性质】小数的性质有以下两条：

　　（1）在小数的末尾添上或者去掉几个零，小数的大小不变。

　　（2）把小数点向右移动n位，小数就扩大10n倍；把小数点向左移动n位，小数就缩小10n倍。

　　【分数基本性质】一个分数的分子和分母都乘以或者都除以同一不为零的数，分数的大小不变。即

　　　

　　【去九数的性质】用9去除一个数，求出商后余下的数，叫做这个数的“去九数”，或者叫做“9余数”。求一个数的“去九数”，一般不必去除，只要把该数的各位数字加起来，再减去9的倍数，就得到该数的“去九数”。（求法见本书第一部分“（四）法则、方法”“2．运算法则或方法”中的“弃九验算法”词条。）去九数有两条重要的性质：

　　（1）几个加数的和的去九数，等于各个加数的去九数的和的去九数。

　　（2）几个因数的积的去九数，等于各个因数的去九数的积的去九数。

　　这两条重要性质，是用“弃九验算法”验算加、减、乘、除法的依据。

　　【自然数平方的性质】

（1）奇数平方的性质。任何一个奇数的平方被8除余1。

　　为什么有这一性质呢？这是因为奇数都可以表示为2k+1的形式，k为整数。而

　　（2k+1）₂=4k₂+4k+1

　　=4k（k+1）+1

　　k与k+1又是连续整数，其中必有一个是偶数，故4k（k+1）是8的倍数，能被8整除，所以“4k（k+1）+1”，即（2k+1）₂能被8除余1，也就是任何一个奇数的平方被8除余1。

　　例如，27₂=729

　　729÷8=91……1

（2）偶数平方的性质。任何一个偶数的平方，都是4的倍数。

　　这是因为偶数可以用2k（k为整数）表示，而（2k）₂＝4k₂

　　显然，4k₂是4的倍数，即偶数的平方为4的倍数。

　　例如，216₂=46656

　　46656÷4=11664

　　即 4|46656

　　【整数运算奇偶性】整数运算的奇偶性有以下四条：

　　（1）两个偶数的和或差是偶数；两个奇数的和或差也是偶数。

　　（2）一个奇数与一个偶数的和或差是奇数。

　　（3）两个奇数之积为奇数；两个偶数之积为偶数。

　　（4）一个奇数与一个偶数之积为偶数。

　　由第（4）条性质，还可以推广到:

　　若干个整数相乘，只要其中有一个整数是偶数，那么它们的积就是个偶数。

　　【偶数运算性质】偶数运算性质有：

　　（1）若干个偶数的和或者差是偶数。

　　（2）若干个偶数的积是偶数。

　　例如，四个偶数38、126、672和1174的和，是偶数2010；用偶数相减的算式3756-128-294-1350的差，也是偶数1984。

　　【奇数运算性质】奇数运算性质有：

　　（1）奇数个奇数的和（差）是奇数；偶数个奇数的和（差）是偶数。

　　（2）若干个奇数的积是奇数。

27、数的大小概念

　　【比较分数大小】用常规方法比较分数大小，有时候速度很慢。采用下述办法，往往可大大提高解题的速度。

　　（1）交叉相乘。把要比较大小的两个分数的分子分母交叉相乘，然后

　　

　　

　　2×5＝10， 3×3=9， 3×8=24， 5×5=25，

　　

　　之所以能这样比较，是由于它们通分时，公分母是分母的乘积。这时，分数的大小就只取决于分子的大小了。

　　（2）用“1”比较。当两个分数都接近1，又不容易确定它们的大小

　

　

　　

　　

　　

　

　　

　　（4）化相同分子。把分子不同的分数化成同分子分数比较大小。有时

序排列起来：

　　

　　（5）两分数相除。用两个分数相除，看它们的商是大于1还是小于1，往往能快速地找出它们的大小关系。由于这样做，省略了通分的过程，所以

　　

　　显然，将它们反过来相除，也是可以的：

　　

【巧比两数大小】若甲、乙两数间的关系未直接给出，比较它们的大小，有一定难度。这时，可按下面的办法去做：

　　（1）先看分子是1的情况。例如下题：

　　

　　第一种方法是直观比较。先画线段图（图4.4）：

　　由对线段图的直观比较可知，乙数大于甲数。

　　

　

　

　　

数。

　　

可知

　　

　　

　　（2）再看分子不是1的情况。例如下题：

　　

　　它同样也可以用四种方法比较大小。比方

　　用直观比较方法，可画线段图如下（图4.5）：

　　由图可知，甲数大于乙数。

　　用统一分子的方法，也可比较它们的大小。因为

　　

　　用图表示就是图4.6：

　　这就是说，把甲数分为9份，乙数分为8份，它们的6份相等。所以，它们每一份也相等。而甲数有9份，乙数只有8份，故甲数大于乙数。

　　

去，即可知道甲数大于乙数。

　　如果用转化关系式比较。由题意可知

　　

　　根据一个因数等于积除以另一个因数，可得

　　

28、数的大小比较

　　【分数、小数大小比较】

　　

　　（全国第二届“华杯赛”决赛口试试题）

　　讲析：这两个分数如果按通分的方法比较大小，计算将非常复杂。于是可采用比较其倒数的办法去解答。倒数大的数反而较小。

　　

　　

　　

　　

　

个数是______。

　　（1992年全国小学数学奥林匹克决赛试题）

　　讲析：将给出的六个数分别写成小数，并且都写出小数点后面前四位数，则把这六个数按从大到小排列是：

　　

　　

　　

　　【算式值的大小比较】

　　例1 设A=9876543×3456789； B=9876544×3456788。

　　试比较A与B的大小。

　　（1990年《小学生数学报》小学数学竞赛试题）

　　讲析：可将A、B两式中的第一个因数和第二个因数分别进行比较。这时，只要把两式中某一部分变成相同的数，再比较不同的数的大小，这两个算式的大小便能较容易地看出来了。于是可得

　　A =9876543×（3456788＋1）

　　=9876543×3456788＋9876543；

　　B =（9876543＋1）×3456788

　　=9876543×3456788＋3456788；

　　所以，A＞B。

　　例2 在下面四个算式中，最大的得数是算式______。

　　

　　（1992年全国小学数学奥林匹克决赛试题）

　　讲析：如果直接把四个算式的值计算出来，显然是很麻烦的，我们不妨运用化简繁分数的方法，比较每式中相同位置上的数的大小。

　　

　　　

　　

　　

　　比较上面四个算式的结果，可得出最大的得数是算式（3）。

　　例3 图5.1中有两个红色的正方形和两个蓝色正方形，它们的面积

　　问：红色的两个正方形面积大还是蓝色的两个正方形面积大？

　　（全国第四届“华杯赛”决赛口试试题）

　　讲析：

　　

方形放入大正方形中去的办法，来比较它们的大小（如图5.2）。

　

　　

　　

　　所以，两个蓝色正方形的面积比两个红色正方形的面积大。

29、实践与实际操作

　　【最短路线】

　　例1 一只蚂蚁要从A处出发，经粘合在一块木板上的正方体（如图5.74）的表面爬到B处。

　　请你在图上画出最短的路线（看得见的画实线，看不见的画虚线），有几条就画几条。

　　（1990年“新苗杯”小学数学竞赛试题）

　　讲析：可将正方体的几个面，按正视位置的前面—上面展开，前面—右面展开，左面—后面展开，左边—上面展开，其展开图都是由两个正方形面组成的长方形（如图5.75所示）。

　　根据两点之间直线段最短的原理，故最短路线为每个长方形对角线，它们共有四条，如图5.76所示。

　　例2 请你在图5.77（3）、（4）、（5）上画出三种与图（2）不一样的设计图，使它们折起来后，都成为图（1）所示的长方形盒子（粗线和各棱交于棱的中点）。

　　（第四届《从小爱数学》邀请赛试题）讲析：解题的关键，是要分清实线与虚线，然后思考它们是按什么方式展开的。

　　不难想象，其答案如图（3）、（4）、（5）所示。

　　【切分图形】

　　例1 请将图5.78分成面积相等，形状相同，且每一块中都含有“数学竞赛”字样的四块图形。

　　（“新苗杯”小学数学竞赛试题）

　　讲析：从条件看，所分成的每一块图中，必须有四个小正方形，且只有五种（如图5.79）。

　　根据图中汉字的具体位置，可发现图5.79中图（1）、图（2）明显不合，图（3）、图（4）也不能分成。于是只剩下图（5）。

　　进一步搜索，便可得到答案。答案如图5.80所示。

　　例2 在一张正方形纸上画两个三角形，最多可以把这个正方形分成________块，画三个三角形，最多可以把这个正方形分成________块；画四个三角形，最多可以把这个正方形分成_________块。

　　（1990年无锡市小学数学竞赛试题）

　　讲析：可先找出规律。

　　在正方形纸上，画一个三角形，依次画三条边时，增加了（1＋1＋1）块，最多可把它分成4块；画二个三角形，依次画三条边时，增加了（3＋3＋3）块，共13块；画三个三角形，依次画三条边时，增加了（5＋5＋5）块，共28块，如图5.81所示。

　　由此推得，画四个三角形，可增加（7＋7＋7）块，最多，共49块。

　　【拼合图形】

　　例1 图5.82是由图5.83中的六块图形拼合而成的，其中图①放在中间一列的某一格。请在图5.82中找出这六个图形，并画出来。

　　（1993年全国小学数学奥林匹克总决赛试题）

　　讲析：可先确定图①的位置。因为图①在中间的一列的某一格，当图①放在A、B、C处时，经试验，与其它五图不能拼成图5.82。

　　当图①放在D处时，这六幅图可以拼成图5.82。拼法如图5.84所示。

　　例2 7块正方体积木堆在桌上。

　　从东、南、西、北四个方向看去，所看到的一面都只有5个正方形，而且看到的图案是一样的。（如图5.85）。那么从上面看下去，看到的图形可能是什么

　　样的？请在图5.86中正确的图形下面打

　　“√”，错误的图形下面打“×”。（《从小爱数学》邀请赛第五届试题）

　　讲析：上面的七幅图都是俯视图。在看每幅图是否正确时，关键是想象出将另两块积木，放在这五块中哪两块的上面，然后分别从东西南北四个方向去看，得出的图形是否与图5.85相吻合。

　　经试验，得出的答案如图5.86所示，即按从左往右，从上至下的位置，依次为√、√、×、√、×、√、√。

省工省时问题

　　例1 某车队有4辆汽车，担负A、B、C、D、E、F六个分厂的运输任) N/ ?+ O# T- ~5 U5 ^+ s5 w
　　（图5.97所标出的数是各分厂所需装卸工人数）。若各分厂自派装卸工，则共需33人。若让一部分人跟车装卸，在需要装卸工人数较多的分厂再配备一个或几个装卸工，那么如何安排才能既保证各分厂所需工人数，又使装卸工人数最少？

　

　　（1990年《小学生报》小学数学竞赛试题）
　　讲析：可从需要工人数最少的E分厂着手。假定每辆车上配备3人，则需在D、C、B、A、F五处分别派1、5、2、3、4人，共需27人。* Z3 d, m7 Q6 s. H/ [
　　若每车配备4人，则需在C、B、A、F四处分别派4、1、2、3人，共需26人。# u; t% t' S4 n) d, Y1 `* d
　　若每车配备5人，则需在C、A、F三处分别派3、1、2人，共需26人。
　　所以，上面的第二、三种方案均可，人数为26人。& WD4 p4 u. a) }4 k" E) w" e3 c
　　例2 少先队员在植树中，每人植树2棵。如果一个人挖一个树坑需要25分钟，运树苗一趟（最多可运4棵）需要20分钟，提一桶水（可浇4棵树）需要10分钟，栽好一棵树需要10分钟，现在以两个人为一个小组进行合作，那么，完成植树任务所需的最短时间是______分钟。
　　（福州市鼓楼区小学数学竞赛试题）
　　讲析：可将甲、乙两人同时开始劳动的整个过程安排，用图5.98来表示出来。5 g1 d; d) y1 x- ?- o, O6 J

　　

　　由图可知，完成任务所需的最短时间，是85分钟。0 h2 Q* h0 `D4 A, g1 I$ A
　　例3 若干箱同样的货物总重19.5吨，只知每箱重量不超过353千克。今有载重量为1.5吨的汽车，至少需要______辆，才能保证把这些货物一次全部运走。（箱子不能拆开）/ x- |$ m+ ~! p% p
　　（北京市第七届“迎春杯”小学数学竞赛试题）
　　讲析：关键是要理解“至少几辆车，才能保证一次运走”的含义。也就是说，在最大浪费车位的情况下，最少要几辆车。
　　∵这堆货物箱数至少有：2 v% \- b' {6 B" s: A) e
　　19500÷353≈55.2≈56（箱）；; l- \0 ^8 b: z8 V7 `
　　一辆汽车每次最多能装的箱数：
　　1500÷353≈4.2≈4（箱）。
　　∴一次全部运走所有货物，至少需要汽车56÷4=14（辆）。8 u' ~3 l+ bqZ4 o
　　例4 如图5.99，一条公路（粗线）两侧有7个工厂（01、02、……、07），通过小路（细线）分别与公路相连于A、B、C、D、E、F点。现在要设置一个车站，使各工厂（沿小路和公路走）的距离总和越小越好。这个车站应设在一______点。
　　（1992年福州市小学数学竞赛试题）7 E6 xu* ~. C" E* a/ ]6 x

　　

　　讲析：从各工厂到车站，总是先走小路，小路的总长不变，所以问题可转化为：“在一条公路上的A、B、C、D、E、F处各有一个工厂，D处有两个工厂。要在公路上设一个站，使各厂到车站的距离总和最小（如图5.100）。; D& Q6 |9 Y; d# ?# m

　　

　　显然，车站应设在尽量靠七个厂的中间部位。
　　如果车站设在D处，则各厂到D总长是：6 K5 j7 X- P4 W; e
　　（DA＋DF）＋（DB＋DE）＋DC=AF＋BE＋DC；
　　如果车站设在C处，则各厂到C总长是
　　（CA＋CF）＋（BC＋CE）＋2·DC＝AF＋BE＋2·DC。9 k\6 h1 z4 k! f2 Gk
　　比较上面两个式子得：当车站设在D处时，七厂到车站的距离总和最小。8 S. E2 z0 ~2 `+ P0 o. P; _# @
【费用最少问题】
　　例1 在一条公路上每隔100千米有一个仓库（如图5.101），共有五个仓库。一号仓库存有10吨货物，二号仓库存有20吨货物，五号仓库存有40吨货物，其余两个仓库是空的。现在想把所有的货物集中存放在一个仓库里，如果每吨货物运输1千米需要0.5元的运费，那么最少要花多少运费才行？$ I/ }5 S% x8 H: a. ^% e- p8 B
　　（全国第一届“华杯赛”复赛试题）

　　

　　讲析：这类问题思考时，要尽量使运这些货物的吨千米数的和最小。处理的方法是：“小往大处靠”。/ K* m9 ?- G2 R6 E
　　因为第五个仓库有40吨，比第一、二仓库货物的总和还多。所以，尽量把第五个仓库的货不动或者动得最近。
　　当存放站设在第四仓库时，一、二、五仓库货物运输的吨千米数为：
　　10×300＋20×200＋40×100=11000；
　　当存放站设在第五仓库时，一、二仓库货物运输的吨千米数为：
　　10×400+20×300=10000。
　　所以，存放点应设在第五号仓库，运费最少。运费是0.5×10000=5000（元）。
　　例2 有十个村，坐落在从县城出发的一条公路上（如图（5.102，单位：千米），要安装水管，从县城送自来水到各村，可用粗细两种水管，粗管足够供应所有各村用水，细管只能供一个村用水，粗管每千米要用8千元，细管每千米要用2千元。把粗管细管适当搭配，互相连接，可降低工程总费用。按最节省的办法，费用应是多少？7 ?& Z5 D/ i4 i8 S6 ]
　　（全国第一届“华杯赛”决赛第二试试题）$ Jy; M+ Q' I, ~* Y5 b1 {

　　

　　讲析：因为粗管每千米的费用是细管的4倍，所以应该在需要安装四根或四根以上水管的地段，都应安装粗管。因此，只有到最后三个村安装细管，费用才最省。
　　不难求出，最少费用为414000元。" S# k0 f`: Z4 X. n1 o- N% [

30、容斥原理问题

　　例1 在1至1000的自然数中，不能被5或7整除的数有______个。

　　（莫斯科市第四届小学数学竞赛试题）

　　讲析：能被5整除的数共有1000÷5=200（个）；

　　能被7整除的数共有1000÷7=142（个）……6（个）；

　　同时能被5和7整除的数共有1000÷35=28（个）……20（个）。

　　所以，能被5或7整除的数一共有（即重复了的共有）：

　　200＋142—28=314（个）；

　　不能被5或7整除的数一共有

　　1000—314=686（个）。

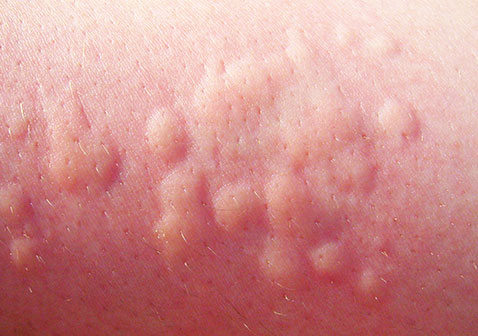
　　例2 某个班的全体学生进行短跑、游泳、篮球三个项目的测试，有4名学生在这三个项目上都没有达到优秀，其余每人至少有一个项目达到了优秀。这部分学生达到优秀的项目、人数如下表：

　　

　　求这个班的学生人数。

　　（全国第三届“华杯赛”复赛试题）

　　讲析：如图5.90，图中三个圆圈分别表示短跑、游泳和篮球达到优秀级的学生人数。

　　

　　只有篮球一项达到优秀的有

　　15—6—5+2=6（人）；

　　只有游泳一项达到优秀的有

　　18—6—6+2=8（人）；

　　只有短跑一项达到优秀的有

　　17—6—5＋2=8（人）。

　　获得两项或者三项优秀的有

　　6＋6+5—2×2=13（人）。

　　另有4人一项都没获优秀。

　　所以，这个班学生人数是13＋6＋8＋8＋4=39（人）。

31、奇数偶数与奇偶性分析

　　【奇数和偶数】

　　例1 用l、2、3、4、5这五个数两两相乘，可以得到10个不同的乘积。问乘积中是偶数多还是奇数多？

　　（全国第二届“华杯赛”决赛口试试题）

　　讲析：如果两个整数的积是奇数，那么这两个整数都必须是奇数。在这五个数中，只有三个奇数，两两相乘可以得到3个不同的奇数积。而偶数积共有7个。所以，乘积中是偶数的多。

　　例2 有两组数，甲组：1、3、5、7、9……、23；乙组：2、4、6、8、10、……24，从甲组任意选一个数与乙组任意选出一个数相加，能得到______个不同的和。

　　（《现代小学数学》邀请赛试题）

　　讲析：甲组有12个奇数，乙组有12个偶数。甲组中任意一个数与乙组中任意一个数相加的和，必为奇数，其中最大是47，最小是3。

　　从3到47不同的奇数共有23个。

　　所以，能得到23个不同的和。

　　本题中，我们不能认为12个奇数与12个偶数任意搭配相加，会得到12×12=144（个）不同的和。因为其中有很多是相同的。

　　【奇偶性分析】

　　例1 某班同学参加学校的数学竞赛。试题共50道。评分标准是：答对一道给3分，不答给1分，答错倒扣1分。请你说明：该班同学得分总和一定是偶数。

　　（全国第三届《从小爱数学》邀请赛试题）

　　讲析：如果50道题都答对，共可得150分，是一个偶数。每答错一道题，就要相差4分，不管答错多少道题，4的倍数总是偶数。150减偶数，差仍然是一个偶数。

　　同理，每不答一道题，就相差2分，不管有多少道题不答，2的倍数总是偶数，偶数加偶数之和为偶数。

　　所以，全班每个同学的分数都是偶数。则全班同学的得分之和也一定是个偶数。

　　例2 5只杯子杯口全都朝上。规定每次翻转4只杯子，经过若干次后，能否使杯口全部朝下？

　　（美国小学数学奥林匹克通讯赛试题）

　　讲析：一只杯口朝上的杯子，要想使杯口朝下，必须翻转奇数次。要想5只杯口全都朝上的杯子，杯口全都朝下，则翻动的总次数也一定是奇数次才能办得到。

　　现在每次只翻转4只杯子，无论翻多少回，总次数一定是偶数。

　　所以，不能使杯口全部朝下。

　　例3 某班共有25个同学。坐成5行5列的方阵。我们想让每个同学都坐到与他相邻的座位上去。（指前、后、左、右），能否做得到？

　　（广州市小学数学竞赛预赛试题）

　　讲析：如图5.44，为了方便，我们将每一格用A或B表示，也就是与A相邻的用B表示，与B相邻的用A表示。

　　要想使每位同学都坐到相邻座位上去，也就是说坐A座位的同学都要坐到B座位上去，而坐B座位上的同学都要坐到A座位上去。

　　但是，A座位共13个，而B座位共12个，所以，不管怎样坐，要想坐A座位的同学都坐到B座位上去，是办不到的。

　　例4 线段AB的两个端点，一个标以红色，一个标以蓝色。在线段中间插入1991个分点，每个分点随意标上红色或蓝色。这样分得1992条不重叠的小线段，如果把两端点颜色不同的小线段叫做标准线段，那么标准线段的条数是奇数还是偶数？

　　（1992年长沙市小学数学竞赛预选赛试题）

　　讲析：每插入一个点，无论其颜色怎样，其非标准线段的条数增加0条或2条，所以插入1991个点后，非标准线段增加总数是一个偶数。又原非标准线段条数为1，是一个奇数，故最后得到的非标准线段必为奇数。

　　非标准线段条数+标准线段条数=1992条。

　　所以，标准线段的条数是奇数。

32、其他定理或性质

　　【算术基本定理】任意一个大于1的整数，都能表示成若干个质数的乘积，如果不计质因数的顺序，则这个分解式是唯一的。即任意一个大于1的整数

　　a=[p₁×p₂×p₃×……×p_n（p₁≤p₂≤p₃≤……≤p_n）其中p₁、p₂、p₃、…、_np都质数；并且若

　　a=q₁×q₂×q₃×…q_m（q₁≤q₂≤q₃≤…≤q_m）

　　其中q₁、q₂、q₃、…、q_m都是质数。那么，m=n，qi=pi（i=1，2，3，…，n）

　　当这个整数是质数时是符合定理的特例。

　　上述定理，叫做“算术基本定理”。

　　【方程同解变形定理】方程的同解变形，有下列两个基本定理：

　　定理一 方程两边同时加上（或同时减去）同一个数或整式，所得的方程与原方程同解。

　　根据这一同解定理，可把方程中某一项改变符号后，从方程的一边移到另一边。这种变形叫做移项。

　　例如，解方程3x=2x+5。

　　解 移项，得

　　3x-2x=5

　　合并同类项，得

　　x=5。

　　定理二 方程两边同时乘以（或除以）同一个不是零的数，所得的方程与原方程同解。

　　

是同解的。

　　【一笔画的性质】为掌握“一笔画”的性质，先介绍“一笔画”的有关概念。

　　图──用若干条线（不一定是直线段）把一些点连接起来的图形，如图1.7。这些点叫图的顶点，如A、B、C、D；这些线叫图的边，如AB、AC、AD等。

　　点的次--每个点上所连接的线的条数，叫做这个点的“次”。如图1.7中，A点有五条线与它相连，B点有三条线与它相连，则A点的次为5；B点有三条线与它相连，则B点的次为3。

　　奇点--点的次数为奇数，则这个点为“奇点”。如图1.7中的A、B、C、D点，全部都是奇点。

　　偶点--点的次数为偶数，则这个点叫做“偶点”。

　　如图1.8中的B点（4次）、D点（2次），都是偶点。一笔画问题--在图1.8中，能否从A点（或其他点）出发，不重复任一边（点可随便经过若干次）而一笔画出全图的问题，叫做“一笔画问题”（也称“七桥问题”，见本书第九部分“七桥问题”词条）。

　　能一笔画的图形，具有下面两条性质：

　　（1）若一个图形中，奇点的个数不大于2，则这个图形必能一笔画成，否则就不能画成。

　　例如图1.7中，奇点有A、B、C、D四个，它无论从哪一点出发，都是不可能一笔画成的。而图1.8中，奇点只有A、C两个，它是可以一笔画成的。其画法可如图1.9所示：从A点出发，经1到C，经2到D，经3到B，经4到A，又经5到B，再经6到A，然后经7到C，完成全图。显然，此图的画法并不止于这一种，这只是多种画法中的一种画法。

　　（2）若一个图中没有奇点，那么始点和终点必须重合；若一个图中有两个奇点，则这两个奇点必是起点和终点。

　　例如图1.10中，点A、B、C均为偶点，没有奇点。若从A点出发，按图外箭头所指的方向，经①、②、③、④、⑤，便又回到了A点。这样，A点便既是始点又是终点。而图1.8中有A、C两个奇点，按性质（1）中的画法，可从A点出发，到C点结束，A是始点，C是终点。图1.9（也可以从C点出发，到A点结束，C为始点，A为终点。）

平移变换

　　【平移线段】有些几何问题，通过线段的上、下、左、右平移以后，能使问题很快地得到正确的解答。

　　例如，下面的两个图形（图4.17和图4.18）的周长是否相等？

　　单凭眼睛观察，似乎图4.18的周长比图4.17的要长一些。但把有关线段平移以后，图4.18就变成了图4.19，其中的线段，有的上移，有的左移，有的右移，它可移成一个正方形。于是，不难发现两图周长是相等的。

　

　　【平移空白或阴影部分】有些求阴影部分或空白部分面积的几何题，采用平移空白部分或平移阴影部分的办法，往往能化难为易，很快使问题求得解答。例如，计算图4.20中阴影部分的面积。

　

　　

圆面积”，然后相加，得整个阴影部分的面积。这显然是很费时费力的。但认真观察一下就会发现，图4.20左半左上部的空白部分，与右半左上部的阴影部分大小一样，只需将右半左上部的阴影部分，平移到左半左上部的空白部分，所有的阴影部分便构成一个正方形了（如图4.21）。所以，阴影部分的面积很快就可求得为5×5=25。

　　又如，一块长30米，宽24米的草地，中间有两条宽2米的走道，把草地分为四块，求草地的面积（如图4.22）。

　　这只要把丙向甲平移靠拢，把丁向乙平移靠拢，题目也就很快能解答出来了。（具体解法略）

33、平面图形的计算

【周长的计算】

　　例1有9个同样大小的小长方形，拼成一个大长方形（如图5.54）的面积是45厘米²，求这个大长方形的周长。

　　（第四届《小学生数学报》邀请赛决赛试题）

　　讲析：设每个小长方形的长是a厘米，宽是b厘米。于是有

　　a×b=45÷9＝5；

　　又有：4a=5b。

　　可求得b=2，a=2.5。

　　所以大长方形的周长为6a＋7b=29（厘米）。

　　例2 图5.55中图（1）和图（2）是两个形状、大小完全相同的大长方形，在每个大长方形内放入四个如图（3）所示的小长方形，斜线区域是空下来的地方，已知大长方形的长比宽多6厘米，问：图（1），图（2）中画斜线的区域的周长哪个大？大多少？（全国第四届“华杯赛”决赛试题）

　　讲析：图5.55（1）中画斜线区域的周长恰好等于大长方形的周长，图5.55（2）中画斜线区域的周长明显比大长方形周长小。二者相差2·AB。

　　从图5.55（2）的竖直方向看，AB＝a－CD

　　图5.55（2）中大长方形的长是a＋2b，宽是2b＋CD，

　　所以，（a+2b）-（2b＋CD）=a-CD=6（厘米）

　　故：图5.55（1）中画斜线区域的周长比图5.55（2）中画斜线区域的周长大，大12厘米。

【面积的计算】

　　例1如图5.56，长方形ADEF的面积是16，三角形ADB的面积是3，三角形ACF的面积是4，那么三角形ABC的面积是______。

　　（北京市第十届“迎春杯”小学数学竞赛试题）

　　讲析：连结AE（如图5.57），则三角形AEC的面积是16÷2-4=4。因为△ACF与△AEC等高，且面积相等。所以，CF=CE。

　　同理，△ABE的面积是16÷2-3=5，则BD∶BE=3∶5。即BE=

　　从而，△ABC的面积是16-（3＋4+2.5）=6.5。

　　例2 如图5．58，在等边三角形ABC中，AF=3FB，FH垂直于BC，已知阴影部分的面积为1平方厘米，这个等边三角形的面积是多少平方厘米？

　　（1992年武汉市小学数学竞赛试题）

　　讲析：如图5.59，连接△ABC各边中点，则△ABC被分成了大小相等的四个小三角形。

　　在△DBG中，再连接各边中点，得出将△DBG又分成了四个很小的三角形。

　　经观察，容易得出△ABC的面积为（1×2）×4×4=32（平方厘米）。

　　例3 三条边长分别为5厘米、12厘米、13厘米的直角三角形如图5.60（1），将它的短直角边对折到斜边上去与斜边相重合如图5.60（2）。那么，图5.60（2）中阴影部分（即未被盖住部分）的面积是______平方厘米。

　　（1993年全国小学数学奥林匹克总决赛第一试试题）

　　讲析：如图5.60（2），设EC等于a厘米，那么DE也为a厘米。

　　△ABC的面积等于△ABE的面积加上△AEC的面积。

　　

　　

　　例4 如图5.61，ABCD是一个梯形，已知三角形ABD的面积是12平方厘米，三角形AOD的面积比三角形BOC的面积少12平方厘米，那么梯形ABCD的面积是______平方厘米。

　　（广州市小学数学竞赛试题）

　　讲析：可设△AOD的面积为S₁。

　　则，△BOC的面积为S₁＋12。

　　于是有：S△ABO=S△ABD-S△AOD＝12-S₁，

　　S△ABC=S△ABO+S△BOC=（12-S₁）＋（S₁＋12）

　　=24（平方厘米）。

　　所以，梯形ABCD的面积是24+12=36（平方厘米）。

　　例5 梯形ABCD被两条对角线分成了四个三角形S₁、S₂、S₃、S₄。已知S₁=2厘米²，S₂=6厘米²。求梯形ABCD的面积。

　　（小学数学奥林匹克通讯赛决赛试题）

　　讲析：三角形S₁和S₂都是等高三角形，它们的面积比为2∶6=1∶3；

　　则：DO∶OB=1∶3。

　　△ADB和△ADC是同底等高三角形，

　　所以，S₁=S₃=2厘米²。

　　三角形S₄和S₃也是等高三角形，其底边之比为1∶3，所以S₄∶S₃=1∶

　　所以，梯形ABCD的面积为

　　

　　例6 正方形边长为20厘米（如图5.63），已知DD′=EE′，CE=6厘米。则阴影部分三角形的面积最大值是______平方厘米。

　　（海口市小学数学竞赛试题）

　　讲析：E′点在BE段滑动，D′点在DC段滑动。

　　设DD′长a厘米。

　　D′C=20-a，E′C=a＋6。

　　

　　又因为D′C＋E′C=（20-a）＋（a＋6）=26。

　　运用等周长的长方形面积最大原理，两个数的和一定（等于26），要把这个和分成两个数，使这两个数的积最大，则当20-a=a＋6=13时，即a=7

　　=84.5（平方厘米）。

　　例7 图5.64是一个正方形，图中所标数字的单位是厘米。问：阴影部分的面积是多少平方厘米？

　　（全国第四届“华杯赛”决赛试题）

　　讲析：如图5.65，连接AC，所分成的四个小三角形分别用S₁、S₂、S₃、S₄表示。

　　容易看出S₂和S₃是关于OC为对称轴的对称图形。

　　所以S₂=S₃。

　　从而不难得出S₁、S₂、S₃、S₄四个小三角形面积相等，即每个小三角

　　例8 一个正方形（如图5.66），被分成四个长方形，它们的面积在图中标出（单位：平方米）。图中阴影部分是一个正方形。那么，它的面积是______。

　　（1992年全国小学数学奥林匹克决赛试题）

　　讲析：可将四个长方形分别用A、B、C、D表示（如图5.67），阴影部分是B中的一部分。

　　大正方形的面积为1平方米，所以它的边长为1米。

　　因为长方形C和D的宽相等，所以它们长的比等于面积比。于是得C的

　　

米。

　　例9 把大的正三角形每边8等分，组成图5.68所示的三角形网。如果每个小三角形面积是1，那么图中粗线围成的三角形面积是______。

　　（1988年北京市奥林匹克邀请赛试题）

　　讲析：一般地，关于格点多边形的面积，有下面的公式：

　　

　　这里，格子面积等于小正方形或平行四边形面积，也就是小三角形面积的2倍。

　　题中，格子面积为1×2=2，内部格点数为12，边上格点数为4。

　　所以，粗线围成的面积是

　　

34、判断题的解答

　　【用筛去（消倍）法判断】一个数能否被3整除，本来是不太难的问题。但当一个数比较大时，用各数位上的数相加，速度很慢，而且容易出现口算错误。若用“筛去（消倍）法”来判断，情况就大不一样了。例如

　　（1）判断76935能否被3整除。先直接筛去能被3整除的6、9、3，剩下的7与5，和为3的倍数，所以3|76935（3能整除76935，或76935能被3整除）。

　　（2）判断3165493能否被3整除。先直接筛去3的倍数3、6、9、

能整除3165493，或3165493不能被3整除。）

　　【能否被7整除】一个数能否被7整除，只要把这个数的末位数字截去，再从余下的数中，减去这个末位数字的2 倍，如果这时能看出所得的差能被7整除，则原来的数就能被7整除，否则就不能被7整除；若是仍看不出来，就要继续上述过程，直到能清楚作出判断为止。例如，判断133能否被7整除：

　　因为差数7能被7整除，所以7|133。

　　这是什么原因呢？请看下面的算式：

　　133×2＝（13×10＋3）×2

　　＝13×20＋3×2

　　=13×（21-1）+3×2

　　=13×21－13＋3×2

　　=13×7×3-（13-3×2）

　　显然，13×7×3中有约数7，它能被7整除，故只要检验后面的（13-3×2）能否被7整除就可以了。（原理可见第一部分的整除性定理）

　　如果要判断的数的位数很多，那么，将这种做法一直进行下去就是。例如，判断62433能否被7整除：

　　∵7|42，∴7|62433

　　这样的判定方法可称作“割尾法”。一个数能否被11、13、17和19整除，也可用割尾法去判断。

　　【能否被11整除】判断一个数能否被11整除，可以采用割尾法、奇偶位差法及分节求和法。

　　（1）割尾法。一个数能否被11整除，只要把它的末尾数字截去，从余下的数里减去这个末位数，看所得的差能否被11整除。差能整除的，原来的数就能整除；差不能整除的，原来的数就不能整除。如一次所得的差还看不出能否被11整除，就继续上述过程，直到能作出判断为止。例如，判断2629能否被11整除：

　　因为11｜22，所以11｜2629。

　　之所以能这么判断，原因在于

　　2629=2620+9

　　=262×10+9

　　=262×（11-1）+9

　　=262×11-262+9

　　=262×11-（262-9）

　　在262×11中有因数11，所以只要看（262-9）的差能否被11整除，就可判断原来的2629能否被11整除。

　　而（262-9）的差是253，

　　253=250+3

　　=25×10+3

　　=25×（11-1）+3

　　=25×11-25+3

　　=25×11-（25-3）

　　同样，只要看（25-3）能否被11整除，就会知道253能否被11整除。进而便可知2629能否被11整除了。

　　（2）奇偶位差法。判断一个数能否被11整除，可先分别求出此数的奇位数字之和及偶位数字之和，再求这两个和的差数，若这个差能被11整除，则原来的那个数就能被11整除；否则，原来的数就不能被11整除。例如，判断823724能否被11整除：

　　∵它的奇位数字之和为4+7+2=13（数位数，从右边个位开始往左数），

　　它的偶位数字的和为2+3+8=13

　　两个和的差数是13-13=0（两数不等时用大数减小数）

　　而 11｜0

　　∴11｜823724

　　之所以能这样判断，是因为

　　823，724

　　=8×100，000+2×10，000+3×1，000+7×100+2×10+4

　　=8×（100，001-1）+2×（9，999+1）+3×（1，001-1）+7×（99+1）+2×（11-1）+4

　　=8×100，001+2×9，999+3×1，001+7×99+2×11+[（2+7+4）-（8+3+2）]

　　显然，在前几项中，因数100，001、9，999、1，001、99、11都是11的倍数，故只需检验[（2+7+4）-（8+3+2）]

　　能否被11整除，就可以作出判断了。

　　（3）分节求和法。把一个自然数从右向左每两位截为一节，然后把这些节加起来。若所得的和能被11整除，那么这个数就能被11整除；否则，这个数就不能被11整除。在这一情况下，如果仍不能作出判断，那就继续上述过程，直到清楚地作出判断为止。例如，判断762421能否被11整除：

　　

　　这一判断方法的理由，可见下面的算式：

　　762421=76×10000+24×100+21

　　=76×（9999+1）+24×（99+1）+21

　　=76×9999+76+24×99+24+21

　　=76×9999+24×99+（76+24+21）

　　在前两项中，因数9999和9都能被11整除，所以只需要检验后面的（76+24+21）能否被11整除了。能整除的原数就能被11整除；不能整除的原数，就不能被11整除。

　　【能否被13整除】一个数能否被13整除，可采用“割尾法”判断：截去末位数字，余下的数加上末位数的4倍。所得的和是13的倍数，则这个数就能被13整除，否则，就不能被13整除。要是割尾一次仍不能作出判断，那就继续割尾，直到能作出判断为止。例如，判断364能否被13整除：

　　∵13｜52，∴13｜364。

　　这一判断的理由，可由下式看出：

　　364×4=（36×10+4）×4

　　=36×40+4×4

　　=36×（39+1）+4×4

　　=36×39+36+4×4

　　=36×13×3+（36+4×4）

　　前面的36×13×3中，有约数13，所以作出判断时，只需要检验（36+4×4）是否能被13整除了。

　　【能否被17整除】一个数能否被17整除，同样可用“割尾法”作巧妙而快速地判断。不过，具体地做法有所不同。例如，判断731能否被17整除，判断方法如下：

　　∵17｜68，∴17｜731。

　　这样做的理由，可见下面的算式推导：

　　731×5=（73×10+1）×5

　　=73×50+1×5

　　=73×（51-1）+1×5

　　=73×51-73+1×5

　　=73×17×3-（73-1×5）

　　由于前面的73×17×3有约数17，故只需检验（73-1×5）能否被17整除，就知道“731×5”能否被17整除。知道“731×5”能否被17整除，也就是知道731能否被17整除了（根据整除性定理）。

　　若是“割尾”一次仍不能作出判断，那就依法继续割尾下去，直到能作出判断为止。例如，判断279191能否被17整除， 可以作如下割尾判断：

　　∵17｜17，∴17｜279191

　　【能否被19整除】一个数能否被19整除，也是可用“割尾法”作巧妙判断的，具体做法如

　　判断475能否被19整除：

　　∵19｜57，∴19｜475。

　　其中的道理，可见下面的算式推导：

　　475×2=（47×10+5）×2

　　=47×20+5×2

　　=47×（19+1）+5×2

　　=47×19+（47+5×2）

　　最后算式中的47×19有约数19，故只需要检验（47+5×2）能否被19整除，就知道“475×2”及“475”能否被19整除了。

　　如果一次“割尾”仍不能作出判断，那就继续“割尾”下去，直至能作出判断为止。例如，判断14785能否被19整除：

排列与组合

【有条件排列组合】

　　例1 用0、1、2、3、4、5、6、7、8、9这十个数字能够组成______个没有重复数字的三位数。

　　（哈尔滨市第七届小学数学竞赛试题）

　　讲析：用这十个数字排列成一个不重复数字的三位数时，百位上不能为0，故共有9种不同的取法。

　　因为百位上已取走一个数字，所以十位上只剩下9个数字了，故十位上有9种取法。

　　同理，百位上和个位上各取走一个数字，所以还剩下8个数字，供个位上取。

　　所以，组成没有重复数字的三位数共有

　　9×9×8=648（个）。

　　例2 甲、乙、丙、丁四个同学排成一排，从左到右数，如果甲不排在第一个位置上，乙不排在第二个位置上，丙不排在第三个位置上，丁不排在第四个位置上，那么不同的排法共有______种。

　　（1994年全国小学数学奥林匹克初赛试题）

　　讲析：因每个人都不排在原来的位置上，所以，当乙排在第一位时，其他几人的排法共有3种；同理，当丙、丁排在第一位时，其他几人的排法也各有3种。

　　因此，一共有9种排法。

　　例3 有一种用六位数表示日期的方法，如890817表示1989年8月17日，也就是从左到右第一、二位数表示年，第三、四位数表示月，第五、六位数表示日。如果用这种方法表示1991年的日期，那么全年中六个数字都不相同的日期共有______天。

　　（1991年全国小学数学奥林匹克决赛试题）

　　讲析：第一、二位数字显然只能取9和1，于是第三位只能取0。

　　第五位数字只能取0、1、2或3，而0和1已取走，当取3时，第六位上只能取0和1，显然不行。因此，第五位上只能取2。

　　于是，第四位上只能取3、4、5、6、7、8；第六位上也只能取3、4、5、6、7、8，且第四、六位上数字不能取同。

　　所以，一共有 6×5=30（种）。

【环形排列】

　　例1 编号为1、2、3、4的四把椅子，摆成一个圆圈。现有甲、乙、丙、丁四人去坐，规定甲、乙两人必须坐在相邻座位上，一共有多少种坐法？

　　（长沙市奥林匹克代表队集训试题）

　　讲析：如图5.87，四把椅子排成一个圆圈。

　　

　　当甲坐在①号位时，乙只能坐在②或④

　　号位上，则共有4种排法；同理，当甲分别坐在②、③、④号位上时，各有4种排法。

　　所以，一共有16种排列法。

　　例2 从1至9这九个数字中挑出六个不同的数填在图5.88的六个圆圈中，使任意相邻两个圆圈内数字之和都是质数，那么最多能找出______种不同的挑法来。（挑出的数字相同，而排列次序不同的都只算一种）

　　

　　（北京市第九届“迎春杯”小学数学竞赛试题）

　　讲析：在1至9这九个自然数中，奇数有1、3、5、7、9五个，偶数有2、4、6、8四个。要使排列之后，每相邻两个数字之和为质数，则必须奇数与偶数间隔排列，也就是每次取3个奇数和3个偶数。

　　从五个奇数中，取3个数共有10种方法；

　　从四个偶数中，取3个数共有4种方法。

　　但并不是每一种3个奇数和3个偶数都可以排成符合要求的排列。经检验，共有26种排法。

35、逻辑思路

　　“逻辑思路”，主要是指遵循逻辑的四大基本规律来分析推理的思路。

　　【同一律思路】同一律的形式是：“甲是甲”，或“如果甲，那么甲”。它的基本内容是，在同一思维过程中，同一个概念或同一个思想对象，必须保持前后一致性，亦即保持确定性。这是逻辑推理的一条重要思维规律。运用这一规律来解题，我们把它叫同一律思路。

　　例1 某公安人员需查清甲、乙、丙三人谁先进办公室，三人口供如下：

　　甲：丙第二个进去，乙第三个进去。

　　乙：甲第三个进去，丙第一个进去。

　　丙：甲第一个进去，乙第三个进去。

　　三人口供每人仅对一半，究竟谁第一个进办公室？

　　分析（用同一律思路推理）；

　　这一类问题具有非此即彼的特点。比如甲是否是第一个进办公室只有两种可能：是或非。我们用1表示“是”，0表示“非”，则可把口供列表处理。

　　（1）若甲第一，则依据丙的口供见左表，这个表与甲的口供仅对一半相矛盾；

　　（2）若甲非第一，则依据丙的口供，乙第三个进去，进行列表处理如右表，与“三人口供仅对一半”相符。

　

　　从而可以判定，丙最先进入办公室。

　　这个问题也可以不列表而用同一律推理。

　　甲的话第一句对，第二句错，则丙第二，乙不是第三，又不是第二，自然乙第一，甲第二，这个结论与丙说的话“半对半错”不符。因此，有甲的第一句错，第二句对。即乙第三个进去，丙不是第二个，自然是第一个。这个结论与乙的话“半对半错”相符：甲不是第三，丙是第一。并且这个结论与丙的话“半对半错”也相符：甲不是第一，乙是第三。

　　在整个思维过程中，我们对三人的话“半对半错”进行了一一验证，直到都符合题目给定的条件为止。

　　例2 从前一个国家里住着两种居民，一个叫宝宝族，他们永远说真话；另一个叫毛毛族，他们永远说假话。一个外地人来到这个国家，碰见三位居民，他问第一个人：“请问你是哪个民族的人？”

　　“匹兹乌图。”那个人回答。

　　外地人听不懂，就问其他两个人：“他说的是什么意思？”

　　第二个人回答：“他说他是宝宝族的。”

　　第三个人回答：“他说他是毛毛族的。”

　　请问，第一个人说的话是什么意思？第二个人和第三个人各属于哪个民族？

　　分析（用同一律思路思考）：

　　如果第一个人是宝宝族的，他说真话，那么他说的是“我是宝宝族的”。如果这个人是毛毛族的，他说假话，他说的还是“我是宝宝族的”。这就是说，第一个人不管是什么民族的，那句话的意思都是：“我是宝宝族的”。

　　根据这一推理，那么第二个人回答“他说他是宝宝族的”这句话是真的，而从条件可知，说真话的是宝宝族人，因此可以判断第二个人是宝宝族人。

　　不管第一个人是什么民族的，根据前面推理已知他说的话是“我是宝宝族的”，而第三个人回答“他说他是毛毛族的”显然是错的，而说假话的是毛毛族人，因此可以断定第三个人是毛毛族人。

　　我们在分析本题时，始终保持了思维前后的一致性，这就是同一律思路的具体运用。

　　【不矛盾律思路】不矛盾律的形式是“甲不是非甲”。它的基本内容是：同一对象，在同一时间内和同一关系下，不能具有两种互相矛盾的性质，它是逻辑推理的又一重要规律，运用不矛盾律来推理、思考某些问题的解答，这种思路我们把它叫做不矛盾律思路。

　　例1 有三个和尚，一个讲真话，一个讲假话，另外一个有时讲真话，有时讲假话。一天，一位智者遇到这三个和尚，他先问左边的那个和尚：“你旁边的是哪一位？”和尚回答说“讲真话的。”他又问中间的和尚：“你是哪一位？”和尚答：“我是半真半假的。”他最后问右边的和尚：“你旁边是哪一位？”答：“讲假话的。”根据他们的回答，智者马上分清了他们，你能分清吗？

　　分析（运用不矛盾律思路探讨）：

　　两件相互矛盾对立的事情，如果一件是不正确的，另一件就是正确的，这就是不矛盾律的基本思路。我们先假设左边和尚讲的是真的，那么中间的和尚是讲真话的，但这与他的回答：“我是半真半假的”矛盾，所以左边和尚讲真话这一假设不对。从而左边和尚讲的是假话，他一定不是讲真话的和尚。中间那个和尚也一定不是讲真话的，所以右边的和尚是讲真话的和尚。根据他的话，中间是讲假话的和尚，剩下左边的和尚自然就是半真半假的。

　　例2 一次学校举行田径运动会，A、B、C、D、E五个班取得了团体前五名，发奖后有人问他们的名次，回答是：

　　A班代表说：“B是第三名，C是第五名。”

　　B班代表说：“D是第二名，E是第四名。”

　　C班代表说：“A是第一名，E是第四名。”

　　D班代表说：“C是第一名，B是第二名。”

　　E班代表说：“D是第二名，A是第三名。”

　　最后，他们都补充说：“我的话是半真半假的。”请你判断一下，他们各个班的名次。

　　分析（用不矛盾律思路分析）：

　　先简化一下记法，比如B班是第三名，则写成B-3，其它类似，这样五个班代表的讲话可简记为：

　　（1）B-3，C-5。

　　（2）D-2，E-4。

　　（3）A-1，E-4。

　　（4）B-2，C-1。

　　（5）A-3，D-2。

　　假设（1）的前半句是真的，即B-3，那么由（4）有C-1，由（3）知A-1不对，有E-4；再由（2）知D-2不对，从（5）知A-3，这与假设矛盾，所以（1）中正确的应是C-5，于是由（4）知C-1不对，应该是B-2，进而知（2）D-2不对，有E-4，并知（5）D-2不对，有A-3，最后只剩下D及第一名，所以知道D应为第一名。

　　最后排出名次自然就非常简单了。

　　上述叙述虽然简化了记号，但文字表述仍然觉得累赘，所以还可以借助图表表达上述推理过程。

　　如图2.21，假设B-3，在B上画一个圆圈（左图），表示推理的起点，找到另一个B，则应是不对的，画一个“×”，再找与这个B同行的“C”，它应是对的，画一个“√”，找与C同列的“A”，它不对，画一个“×”，等等。最后A-3被画了一个“√”，这与B-3相矛盾，故B-3是错的。在这个“B”上画一个“×”，重新开始推理（右图）。

　

　　从（1）的C开始，因B-3是错的，则C-5记“√”，则（4）中C-1画“×”，B-2记“√”，由此推出（5）D-2记“×”，（2）D-2记“×”，……从表中可以看出，B-2，A-3、E-4、C-5，那么谁是第一，表中虽然未表达，但明眼人一看就知道了。

　　【排中律思路】排中律的形式是“或者是甲，或者是非甲”。它的基本内容是：同一对象在同一时间内和同一关系下，或者是具有某种性质。或者是不具有某种性质，二者必居其一，不能有第三种情况。它是处理肯定判断与否定判断之间的关系的一个规律。运用这一规律来推理的思路，我们把它叫排中律思路。

　　排中律和不矛盾律的基本作用是相同的，即都是排除思想中的矛盾。但也有区别：一是适用范围不同，不矛盾律的适用范围宽，既适用于互相反对的判断，也适用于互相矛盾的判断，排中律的作用范围窄些，只适用于互相矛盾的判断，不适用互相反对的判断；二是要求不同，不矛盾律要求对互相反对的和互相矛盾的判断，不能同时断定其中每一个都是真的，因为其中至少有一个是假的。排中律则要求：对于互相矛盾的判断，必须肯定其中一个是真，因为其中必有一真，不能都假。如果我们确定了某一个是正确的，根据不矛盾律，就可以得出另一个是错误的。反过来。如果我们确定了某一个是错误的，根据排中律，就可以得出另一个是正确的。从这方面来看，如果说不矛盾律提供我们逻辑否定的基础，那么排中律则主要提供我们逻辑肯定的基础；三是逻辑错误性质不同，不矛盾律要求的逻辑错误是“自相矛盾”，排中律要求的逻辑错误是“模棱两不可”。

　　例1 老师有一黑两白三顶帽子，给两个学生看后，让他们闭上眼睛，从中取出两顶给他们戴上，然后让他们睁开眼睛，互相看清对方戴的帽子，并立即说出自己头上戴的帽子是什么颜色，两位同学都不能立即说出，请问你知道这两位学生戴的各是什么颜色的帽子吗？

　　分析（运用排中律思路思索）：

　　假设你是这两个学生中的一个，因为你知道只有一顶黑帽子，当你看到对方戴的是黑帽子时，你能判断自己戴的帽子颜色吗？可以的，根据排中律：“非此即彼”，你一定会推断出自己戴的是白帽子。

　　现在两个学生都不能利用排中律很快地说出自己戴的是白帽子，说明他们两人都没有看见黑帽子，由此断定，老师给两位学生戴的是两顶白帽子。

　　例2 曾实、张晓、毛梓青在一起，一位是工程师、一位是医师、一位是教师。现在只知道：

　　（1）毛梓青比教师年龄大；

　　（2）曾实和医师不同岁；

　　（3）医师比张晓年龄小。

　　你能确定谁是工程师？谁是医师？谁是教师吗？

　　分析（沿着排中律思路探索）：

　　根据排中律的要求，如果我们能确定某个是错误的，就可以得出另一个是正确的。现在已知（1）曾实和医师不同岁，（2）医师比张晓年龄小，就可以判定曾实和张晓都不是医师，因此只有毛梓青是医师；

　　若张晓是教师，则根据（1）毛梓青比教师年龄大，即毛梓青比张晓年龄大，与（3）医师比张晓年龄小，即毛梓青比张晓年龄小，这两个结论是互相矛盾的，因此张晓不可能是教师。张晓既不是医师（因为毛梓青是医师），又不是教师，所以张晓应该是工程师了。因为三个人、三个职业，已经确定了毛梓青是医师，张晓是工程师，剩下的曾实只能是教师了。

　　该题的思路还可以用下表表示：

　　【充足理由律思路】充足理由律的形式是：“所以有甲，是因为有乙”。它的意思是说，任何正确的思想，一定有它的充足理由；任何思想，只有当它具有充足的理由时，这种思想才能被认为是正确的。在数学中，如果由条

　　正确的，A就是B的正确性的充分理由。因此B的正确性要以A的正确性为基础，而要使A的正确性得到确认，又得为它提出充足的理由，照此类推。这样，当我们要论证某一思想是正确的时候，常常要引证一系列的理由。以此连锁引证下去，直到最后的理由——它的正确性已经确定，并且得到普遍承认的。具体说来有下列三种：（1）明显的事实，它可以为人们所直接感知的；（2）公理；（3）科学的规律。当然在实际进行论证时，并不是总要引证到最后的理由，数学中已经证明过的定理、定律、公式、法则等，都可以作为论证所根据的理由。

　　充足理由律是进行推理的基础。运用充足理由律来思考数学问题，我们把它叫做充足理由律思路。

　　例1 200米赛跑，张强比李军快0.2秒，王明的成绩是39.4秒，赵刚的成绩比王明慢0.9秒，但比张强快0.1秒，林林比张强慢3秒，请你给这五人排出名次来。

　　分析（运用充足理由律思路思索）：

　　题中有两种概念。一是成绩好坏，需要进行量的计算；二是快慢关系推理，先用计算量进行比较推理。

　　抓住“各人跑200米需要的时间”为比较量。并设字母A、B、C、D、E来分别表示张强、李军、王明、赵刚、林林的时间。

　　∵王明的成绩是39.4秒，赵刚的成绩比王明慢0.9秒（即C=39.4秒，D=C＋0.9）

　　∴D=39.4+0.9=40.3（秒）

　　又∵ 赵刚比张强快0.1秒（即D＋0.1＝A）

　　∴A=40.3＋0.1=40.4（秒）（传递性）

　　又∵张强比李军快0.2秒（即A=B-0. 2）

　　∴B=A＋0.2=40.4＋0.2=40.6（秒）

　　又∵林林比张强慢3秒（即A=E-0.3）

　　∴E=A＋3=40.4＋3=43.4（秒）

　　由43.4＞40.6＞40.4＞40.3＞39.4

　　即 E＞B＞A＞D＞C

　　谁是第一、谁是第二、第三、第四、第五名，不就一目了然了吗？

　　本题还可以单纯用快慢关系来进行判断。

　　∵ A＜B，D＞C， D＜A， E＞A，

　　可得B、E均＞A＞D＞C，

　　∴一、二、三名分别应是C、D、A。

　　但第四、五名仍需计算。

　　由E=A＋3秒，B=A＋0.2秒，

　　可知E＞B，

　　故 B是第四，E是第五名。

　　例2 填数使下列竖式成立：

　　

　　分析（运用充足理由律思路来探讨这两个式题）：

　　第（1）题。抓住乘、除法法则和乘除的互逆关系去思考。

　　∵( )( )×5=33( )

　　∴只要求得 33( )÷5=( )( )，就可以得出竖式被乘数了，现可知33( )÷5商的十位得6，故被乘数的十位应是6，个位是几呢？

　　再往下看：乘数35的十位数字是3，3与被乘数个位相乘的积的末尾数字要是8，显然只有3与6相乘末尾数字才能是8，所以被乘数是66。

　　找到了被乘数是66以后，其他数字自然就容易找到了。

　　第（2）题仍抓住除法算式特征和乘除的互逆关系去找理由。

　　由除法竖式特征第二次余数为0，只好把被除数十位数和个位数同时移下，故可得y=0。

　　∴x＞8。

　　又∵1≤x≤9，∴x=9，

　　则商数为9807。

　　∴ab≥12。

　　故ab=12。

　　此题确定了商和除数，其他数字自然就容易找了。

36、连续数求和的速算

　　苦干个连续整数求和的问题，可以分为“连续自然数求和”、“连续奇数求和”与“连续偶数求和”三类。

　　【连续自然数求和】几个连续的自然数相加，可以把它们的首项和末项相加，把所得的结果除以2以后，再乘以项数，得到的便是这几个连续自然数的和。

　　例如，13＋14＋15＋16+17+18＋19＋20＋21＋22

　　=（13+22）÷2×10

　　=17.5×10

　　=175

　　如果加数的个数（项数）是奇数（单数），也可以直接用排列在正中间的数（中间项）乘以项数，去求它们的和。例如

　　

　　=15×9 （中间项）

　　=135

　　【连续奇数求和】连续奇数的求和，也可以用上面介绍的“连续自然数求和的速算”方法去速算。例如

　　3+5＋7+ 9＋11＋13+ 15＋17＋19

　　＝（3＋19）÷2×9

　　=11×9

　　=99

　　

　　=11（中间项）×9（项数）

　　=99

　　如果是从1开始的几个连续奇数求和，则可以用这些奇数的个数自乘，便得到这几个连续奇数的和。例如

　　1＋3＋5+ 7＋9＋11=6×6=36（奇数个数是6）

　　1+3＋5＋7＋9＋11＋13＋15＋17＋19＋21

　　=11×11

　　=121。（奇数个数是11）

　　【连续偶数求和】 连续偶数的求和，同样可以用“连续自然数求和的速算”方法速算。例如

　　8＋10＋12＋14＋16＋18+20+22＋24

　　＝（8＋24）÷2×9

　　=144

　　如果连续偶数是从2开始的，即求从2开始的连续偶数之和，则可以用这些偶数的个数乘以个数加1之和，就得到这几个连续偶数的和。例如

　　2＋4＋6＋8＋10=5×（5+1）（偶数个数是5）

　　=30

　　2＋4＋6＋8＋10＋12＋14＋16＋18＋20＋22＋24＋26

　　=13×（13＋1）（偶数个数是13）

　　=182

37、利用间接条件

　　【利用隐含的间接条件】 发现和利用隐含的间接条件来解答题目，往往能克服所学知识不够所造成的困难，大大减少计算的时间。例如

　　如图4.65，已知正方形面积为18平方厘米，求阴影部分的面积。

　　一般解法是用正方形面积，减去圆的面积。但在小学阶段，大家还不会求圆的半径或直径怎么办呢？

　　因为圆面积公式是

　　

　　

刃而解。至于能否求出r或d这样的直接条件，是并不重要的。所以，可以用下面的方法来解答：

　　

便是

　　18-14.3=3.87（平方厘米）

　　

　　

　　阴影部分的面积便是

　　18-14.13=3.87（平方厘米）

　　（3）若把正方形面积扩大2倍，则面积为36平方厘米，新正方形的边长就是6厘米，即随之也扩大了2倍的新圆的直径为6厘米，半径为3厘米。所以随之而扩大了2倍的阴影部分的面积是

　　

　　=7.74（平方厘米）

　　原来的阴影部分的面积便是

　　7.74÷2=3.87（平方厘米）

　　又如，如图4.66，ABCD为矩形，里面有一个最大的半圆，OC=10厘米，求阴影部分的面积。

　　解题时，可将矩形分割为两个小正方形，并连结O、D。因为△DOC是等腰三角形，OC=OD=10厘米，所以

　　

　　

　　

　　故阴影部分的面积便是

　　100-3.14×50÷2＝100-78.5

　　=21.5（平方厘米）

　　【利用定比】 利用题目中不变的“定比”来解题，有时也能使题目得到较快地解答。这也是利用间接条件去解答题目。

　　我们仍以上面的第一个例子（图4.65）为例。按照扩、缩图形的思路，可将它一分为四，得到图4.67。

　

　　

小正方形的面积和阴影部分的面积也会改变。不过，变化中有个不变的因素，即阴影部分面积和小正方形面积之比是不变的。实际上，这也是题目中的一个间接条件。

　　设小正方形边长为a，则阴影部分面积占小正方形面积的

　　

　　所以，原图阴影部分的面积是

　　18÷4×21.5％×4=4.5×21.5％×4

　　=0.9675×4

　　=3.87（平方厘米）

　　或者是18×21.5％=3.87（平方厘米）

　　显然，只要是由这样的基本图形拼合的图形，如以下四图（图4.68），都可用“21.5％”（即21.5∶100）这一定比，去求图中的阴影部分的面积。（解略）

38、立体图形的计算

　　【表面积的计算】

　　例1 一个正方体木块，棱长1米，沿水平方向将它锯成3片，每片又锯成4长条，每条又锯成5小块，共得到大小不等的长方体60块（如图5.69）。那么，这60块长方体的表面积的和是平方米。

　　（1988年北京小学数学奥林匹克邀请赛试题）

　　讲析：不管每次锯的长方体大小如何，横着锯2次一共增加了4个正方形面；前后竖直方向锯3次共增加了6个正方形面；左右竖直方向锯4次共增加了8个正方形面。原来大正方体有6个正方形面，所以一共有24个正方形面。

　　所以，60块长方体的表面积之和是

　　（1×1）×24＝24（平方米）。

　　例2 图5.70是由19个边长都是2厘米的正方体重叠而成的。求这个立体图形的外表面积。

　　（北京市第一届“迎春杯”小学数学竞赛试题）

　　讲析：如果按每一层有多少个正方体，然后再数出每层共有多少个外表面正方形，则很麻烦。于是，我们可采用按不同的方向来观察的方法去计算。

　　俯视，看到9个小正方形面；正视，看到10个小正方形面；侧视，看到8个小正方形面。

　　所以，这个立体图形的表面积是（2×2）×[（9＋10＋8）×2]=216（平方厘米）。

　　【体积的计算】

　　例1 一个正方体的纸盒中恰好能放入一个体积为628立方厘米的圆柱体，如图5.71，纸盒的容积有多大？（π取3.14）

　　（全国第四届“华杯赛”复赛试题）

　　讲析：因圆柱体的高、底面直径以及正方体的棱长都相等。故可设正方

　

　　

　　

　　即：正方体纸盒的容积是800立方厘米。

　　例2 在一个棱长4厘米的正方体的上面、右面、前面这三个面的中心分别挖一个边长1厘米的正方形小孔（如图5. 72所示），并通过对面，求打孔后剩下部分的体积。

　　（北京市第二届“迎春杯”小学数学竞赛试题）。

　　讲析：打完孔之后，在大正方体正中央就有一个1×1×1的空心小正方体。

　　三个孔的体积是（1×1×4）×3-（1×1×1）×2=10（立方厘米）。

　　所以，打孔后剩下部分的体积是4×4×4—10=54（立方厘米）。

　　例3 一个长、宽、高分别是21厘米、15厘米、12厘米的长方体，从它的上面尽可能大地切下一个正方体，然后从剩余部分中再尽可能大地切下一个正方体，最后再从第二次剩余部分尽可能大地切下一个正方体，剩下的体积是多少立方厘米？

　　（北京市第八届“迎春杯”小学数学竞赛试题）

　　讲析：解本题的关键，是要想到每次以哪个边长作棱长去切下正方体。实际上，我们可以将三个数轮换相减，即，在三个数 21、 15、12中，第一次取最小数12为棱长切下一个正方体；第二次取大数与

小数的差21—12=9为棱长切下一个正方体；第三次取15与9的差为棱长切下一个正方体（如图5.73）

　　所以，剩下的体积是

　　21×15×12-（12³+9³+6³)=107（立方厘米）。

39、解应用题的公式

　　【和差问题公式】

　　（和+差）÷2=较大数；

　　（和-差）÷2=较小数。

　　【和倍问题公式】

　　和÷（倍数+1）=一倍数；

　　一倍数×倍数=另一数，

　　或 和-一倍数=另一数。

　　【差倍问题公式】

　　差÷（倍数-1）=较小数；

　　较小数×倍数=较大数，

　　或 较小数+差=较大数。

　　【平均数问题公式】

　　总数量÷总份数=平均数。

　　【一般行程问题公式】

　　平均速度×时间=路程；

　　路程÷时间=平均速度；

　　路程÷平均速度=时间。

　　【反向行程问题公式】反向行程问题可以分为“相遇问题”（二人从两地出发，相向而行）和“相离问题”（两人背向而行）两种。这两种题，都可用下面的公式解答：

　　（速度和）×相遇（离）时间=相遇（离）路程；

　　相遇（离）路程÷（速度和）=相遇（离）时间；

　　相遇（离）路程÷相遇（离）时间=速度和。

　　【同向行程问题公式】

　　追及（拉开）路程÷（速度差）=追及（拉开）时间；

　　追及（拉开）路程÷追及（拉开）时间=速度差；

　　（速度差）×追及（拉开）时间=追及（拉开）路程。

　　【列车过桥问题公式】

　　（桥长+列车长）÷速度=过桥时间；

　　（桥长+列车长）÷过桥时间=速度；

　　速度×过桥时间=桥、车长度之和。

　　【行船问题公式】

　　（1）一般公式：

　　静水速度（船速）+水流速度（水速）=顺水速度；

　　船速-水速=逆水速度；

　　（顺水速度+逆水速度）÷2=船速；

　　（顺水速度-逆水速度）÷2=水速。

　　（2）两船相向航行的公式：

　　甲船顺水速度+乙船逆水速度=甲船静水速度+乙船静水速度

　　（3）两船同向航行的公式：

　　后（前）船静水速度-前（后）船静水速度=两船距离缩小（拉大）速度。

　　（求出两船距离缩小或拉大速度后，再按上面有关的公式去解答题目）。

　　【工程问题公式】

　　（1）一般公式：

　　工效×工时=工作总量；

　　工作总量÷工时=工效；

　　工作总量÷工效=工时。

　　（2）用假设工作总量为“1”的方法解工程问题的公式：

　　1÷工作时间=单位时间内完成工作总量的几分之几；

　　1÷单位时间能完成的几分之几=工作时间。

　　（注意：用假设法解工程题，可任意假定工作总量为2、3、4、5……。特别是假定工作总量为几个工作时间的最小公倍数时，分数工程问题可以转化为比较简单的整数工程问题，计算将变得比较简便。）

　　【盈亏问题公式】

　　（1）一次有余（盈），一次不够（亏），可用公式：

　　（盈+亏）÷（两次每人分配数的差）=人数。

　　例如，“小朋友分桃子，每人10个少9个，每人8个多7个。问：有多少个小朋友和多少个桃子？”

　　解（7+9）÷（10-8）=16÷2

　　=8（个）………………人数

　　10×8-9=80-9=71（个）………………………桃子

　　或8×8+7=64+7=71（个）（答略）

　　（2）两次都有余（盈），可用公式：

　　（大盈-小盈）÷（两次每人分配数的差）=人数。

　　例如，“士兵背子弹作行军训练，每人背45发，多680发；若每人背50发，则还多200发。问：有士兵多少人？有子弹多少发？”

　　解（680-200）÷（50-45）=480÷5

　　=96（人）

　　45×96+680=5000（发）

　　或50×96+200=5000（发）（答略）

　　（3）两次都不够（亏），可用公式：

　　（大亏-小亏）÷（两次每人分配数的差）=人数。

　　例如，“将一批本子发给学生，每人发10本，差90本；若每人发8本，则仍差8本。有多少学生和多少本本子？”

　　解（90-8）÷（10-8）=82÷2

　　=41（人）

　　10×41-90=320（本）（答略）

　　（4）一次不够（亏），另一次刚好分完，可用公式：

　　亏÷（两次每人分配数的差）=人数。

　　（例略）

　　（5）一次有余（盈），另一次刚好分完，可用公式：

　　盈÷（两次每人分配数的差）=人数。

　　（例略）

　　【鸡兔问题公式】

　　（1）已知总头数和总脚数，求鸡、兔各多少：

　　（总脚数-每只鸡的脚数×总头数）÷（每只兔的脚数-每只鸡的脚数）=兔数；

　　总头数-兔数=鸡数。

　　或者是（每只兔脚数×总头数-总脚数）÷（每只兔脚数-每只鸡脚数）=鸡数；

　　总头数-鸡数=兔数。

　　例如，“有鸡、兔共36只，它们共有脚100只，鸡、兔各是多少只？”

　　解一 （100-2×36）÷（4-2）=14（只）………兔；

　　36-14=22（只）……………………………鸡。

　　解二 （4×36-100）÷（4-2）=22（只）………鸡；

　　36-22=14（只）…………………………兔。

　　（答 略）

　　（2）已知总头数和鸡兔脚数的差数，当鸡的总脚数比兔的总脚数多时，可用公式

　　（每只鸡脚数×总头数-脚数之差）÷（每只鸡的脚数+每只兔的脚数）=兔数；

　　总头数-兔数=鸡数

　　或（每只兔脚数×总头数+鸡兔脚数之差）÷（每只鸡的脚数+每只免的脚数）=鸡数；

　　总头数-鸡数=兔数。（例略）

　　（3）已知总数与鸡兔脚数的差数，当兔的总脚数比鸡的总脚数多时，可用公式。

　　（每只鸡的脚数×总头数+鸡兔脚数之差）÷（每只鸡的脚数+每只兔的脚数）=兔数；

　　总头数-兔数=鸡数。

　　或（每只兔的脚数×总头数-鸡兔脚数之差）÷（每只鸡的脚数+每只兔的脚数）=鸡数；

　　总头数-鸡数=兔数。（例略）

　　（4）得失问题（鸡兔问题的推广题）的解法，可以用下面的公式：

　　（1只合格品得分数×产品总数-实得总分数）÷（每只合格品得分数+每只不合格品扣分数）=不合格品数。或者是总产品数-（每只不合格品扣分数×总产品数+实得总分数）÷（每只合格品得分数+每只不合格品扣分数）=不合格品数。

　　例如，“灯泡厂生产灯泡的工人，按得分的多少给工资。每生产一个合格品记4分，每生产一个不合格品不仅不记分，还要扣除15分。某工人生产了1000只灯泡，共得3525分，问其中有多少个灯泡不合格？”

　　解一 （4×1000-3525）÷（4+15）

　　=475÷19=25（个）

　　解二 1000-（15×1000+3525）÷（4+15）

　　＝1000-18525÷19

　　=1000-975=25（个）（答略）

　　（“得失问题”也称“运玻璃器皿问题”，运到完好无损者每只给运费××元，破损者不仅不给运费，还需要赔成本××元……。它的解法显然可套用上述公式。）

　　（5）鸡兔互换问题（已知总脚数及鸡兔互换后总脚数，求鸡兔各多少的问题），可用下面的公式：

　　〔（两次总脚数之和）÷（每只鸡兔脚数和）+（两次总脚数之差）÷（每只鸡兔脚数之差）〕÷2=鸡数；

　　〔（两次总脚数之和）÷（每只鸡兔脚数之和）-（两次总脚数之差）÷（每只鸡兔脚数之差）〕÷2=兔数。

　　例如，“有一些鸡和兔，共有脚44只，若将鸡数与兔数互换，则共有脚52只。鸡兔各是多少只？”

　　解 〔（52+44）÷（4+2）+（52-44）÷（4-2）〕÷2

　　=20÷2=10（只）……………………………鸡

　　〔（52+44）÷（4+2）-（52-44）÷（4-2）〕÷2

　　=12÷2=6（只）…………………………兔（答略）

　　【植树问题公式】

　　（1）不封闭线路的植树问题：

　　间隔数+1=棵数；（两端植树）

　　路长÷间隔长+1=棵数。

　　或 间隔数-1=棵数；（两端不植）

　　路长÷间隔长-1=棵数；

　　路长÷间隔数=每个间隔长；

　　每个间隔长×间隔数=路长。

　　（2）封闭线路的植树问题：

　　路长÷间隔数=棵数；

　　路长÷间隔数=路长÷棵数

　　=每个间隔长；

　　每个间隔长×间隔数=每个间隔长×棵数=路长。

　　（3）平面植树问题：

　　占地总面积÷每棵占地面积=棵数

　　【求分率、百分率问题的公式】

　　比较数÷标准数=比较数的对应分（百分）率；

　　增长数÷标准数=增长率；

　　减少数÷标准数=减少率。

　　或者是

　　两数差÷较小数=多几（百）分之几（增）；

　　两数差÷较大数=少几（百）分之几（减）。

　　【增减分（百分）率互求公式】

　　增长率÷（1+增长率）=减少率；

　　减少率÷（1-减少率）=增长率。

　　

比甲丘面积少几分之几？”

　　解 这是根据增长率求减少率的应用题。按公式，可解答为

　　

百分之几？”

　　解 这是由减少率求增长率的应用题，依据公式，可解答为

　　　

　　【求比较数应用题公式】

　　标准数×分（百分）率=与分率对应的比较数；

　　标准数×增长率=增长数；

　　标准数×减少率=减少数；

　　标准数×（两分率之和）=两个数之和；

　　标准数×（两分率之差）=两个数之差。

　　【求标准数应用题公式】

　　比较数÷与比较数对应的分（百分）率=标准数；

　　增长数÷增长率=标准数；

　　减少数÷减少率=标准数；

　　两数和÷两率和=标准数；

　　两数差÷两率差=标准数；

　　【方阵问题公式】

　　（1）实心方阵：（外层每边人数）²=总人数。

　　（2）空心方阵：

　　（最外层每边人数）²-（最外层每边人数-2×层数）²=中空方阵的人数。

　　或者是

　　（最外层每边人数-层数）×层数×4=中空方阵的人数。

　　总人数÷4÷层数+层数=外层每边人数。

　　例如，有一个3层的中空方阵，最外层有10人，问全阵有多少人？

　　解一 先看作实心方阵，则总人数有

　　10×10=100（人）

　　再算空心部分的方阵人数。从外往里，每进一层，每边人数少2，则进到第四层，每边人数是

　　10-2×3=4（人）

　　所以，空心部分方阵人数有

　　4×4=16（人）

　　故这个空心方阵的人数是

　　100-16=84（人）

　　解二 直接运用公式。根据空心方阵总人数公式得

　　（10-3）×3×4=84（人）

　　【利率问题公式】利率问题的类型较多，现就常见的单利、复利问题，介绍其计算公式如下。

　　（1）单利问题：

　　本金×利率×时期=利息；

　　本金×（1+利率×时期）=本利和；

　　本利和÷（1+利率×时期）=本金。

　　年利率÷12=月利率；

　　月利率×12=年利率。

　　（2）复利问题：

　　本金×（1+利率）^存期期数=本利和。

　　例如，“某人存款2400元，存期3年，月利率为10．2‰（即月利1分零2毫），三年到期后，本利和共是多少元？”

　　解 （1）用月利率求。

　　3年=12月×3=36个月

　　2400×（1+10．2％×36）

　　=2400×1．3672

　　=3281．28（元）

　　（2）用年利率求。

　　先把月利率变成年利率：

　　10．2‰×12=12．24％

　　再求本利和：

　　2400×（1+12．24％×3）

　　=2400×1．3672

　　=3281．28（元）（答略）

　　（复利率问题例略）

40、解一般题用得较多的技巧

　　【巧换角度】 从多种角度去思考、分析复合应用题，不仅可找到多种解题方法，而且还可找到比较巧妙的解法。例如：

　　“挖一段56米长的水沟，每天挖7米，已经挖了5天。照这样计算，剩下的还要挖几天？”

　　按一般思考角度，可先求剩下的长度，再求要挖的天数。如果能换一个角度，先求共要挖的天数，再求还要挖的天数，那么解答起来就既简便，又巧妙了：

　　56÷7-5=8-5

　　=3（天）

　　

了多少名女队员？”

　　如按一般的思考角度，应抓住“女队员人数”去寻找解法和答案。可是这在小学的知识范围内，显然有一定困难，题目似乎是无法可解的。但是，只要转换一个角度，从“男队员人数”方面去思考、分析，前景就“柳暗花明了”：

　　

所以男队员人数是

　　

　　

在有的男女队员总数便是

　　

　　于是，转进来的女队员人数便是

　　250-240=10（名）

　　【巧妙替换】 有些应用题，已给的条件常出现两种或更多种不同属性的量，并且在不同量之间存在有换算关系。这时，暂用其中的一种量去替换另一种量，有时候往往会给题目的解答，带来不少方便。例如

　　“工地用5辆大车和4辆小车一次共运来水泥42.5吨，已知每辆大车比每辆小车多运4吨，每辆大车和每辆小车各运来水泥多少吨？”

　　题目中有两个未知数，解答起来有一定困难。但运用替换方法，把4辆小车换成大车，题目的解答就变得比较容易：

　　设每辆小车都多运4吨，那么小车运的吨数就和大车同样多了（也就是将小车都转换为大车了）。这时，4辆小车就会共增加运量

　　4×4=16（吨）

　　总共运的吨数就会增加到

　　42.5＋16=58.5（吨）。

　　这58.5吨便是（5＋4）辆大车运的水泥数，所以，每辆大车运来的水泥便是

　　58.5÷（5＋4）=58.5÷9

　　=6.5（吨）

　　每辆小车运来的水泥便是

　　6.5-4＝2.5（吨）

　　显然，将大车转换为小车（即将小车去替换大车解题），也是可以的。

　　又如，“买3千克奶糖的钱与买4.8千克水果糖的价钱相等。买4千克巧克力的钱与买6千克奶糖的钱相等。那么，买9千克巧克力的钱可买水果糖多少千克？”

　　题目的条件中没有具体的钱数，可用替换方法去解。但巧克力与水果糖不能直接替换，需要通过奶糖这一中间的“媒介”去进行替换。

　　解题方法可以是：

　　（1）6千克奶糖是3千克奶糖的多少倍？

　　6÷3=2（倍）

　　（2）6千克奶糖可换多少水果糖？

　　4.8×2=9.6（千克）

　　（3）1千克巧克力的钱可买多少水果糖？

　　9.6÷4=2.4（千克）

　　（4）9千克巧克力的钱可以买多少水果糖？

　　2.4×9=21.6（千克）

　　列成综合算式便是

　　4.8×（6÷3）÷4×9=4.8×2÷4×9

　　=9.6÷4×9

　　=21.6（千克）（答略）

　　【巧用等量关系】 有些应用题已知条件间的关系比较复杂。但是，如果能从这些复杂的关系中，找到一种合适的等量关系，则常常可使问题较简捷地解答出来。这是一种力求寻找和巧用最佳等量关系的解题方法。例如

　　“甲乙二人需要做同样多的零件数，甲比乙每天多做5个，乙因病中途休息了3天，所以8天后甲做的零件数刚好是乙做的零件数的2倍。求这时甲乙二人各做的零件个数。”

　　由题中的条件，可以得到两组等量关系：

　　甲每天做的个数-乙每天做的个数=5………①

　　甲8在做的个数=乙8天后做的个数×2………②

　　设甲每天做x个，则乙每天做（x-5）个；

　　设乙每天做x个，则甲每天做（x+5）个。

　　设元列方程以后，若使用等量关系①，很明显，方程的解答是比较繁琐的，因为分数需要通分。于是，我们便选择等量关系②来列方程解题：

　　设乙每天做零件x个，则甲每天做零件（x＋5）个。于是，有方程

　　（x+5）×8=2×（8-3）x

　　

　　进而可知，甲每天做的是 20+5=25（个）

　　8天后甲做的是 25×8=200（个），

　　8天后乙做的是 20×（8-3）=100（个）

　　（答略）

　　　　

36名学生到乙校学习，则甲乙两校学生人数相等。甲乙两校原来各有学生多少？”

　　在题目中，可以找到三组等量关系：

　　甲校原来人数-乙校后来人数=36…………①

　　甲校原来人数-36=乙校原来人数+36…………②

　　

　　经过比较，利用等量关系①列方程解题，显然比较简便：

　　设两校共有x人，可得方程为

　　　

　　

　　

　　乙校原有720-396=324（人） （答略）

　　在利用等量关系解题时，有时候通过“单位1”，可以找到最巧妙的解法。比方下面的这一道工程问题：

　　“一项工程，甲独做24天完成，丙独做40天完成，甲、乙、丙三人合做，10天可以完成。这项工程如果由乙来独做，多少天可以完成？”

　　在题目条件中，我们可以得到下面的两组等量关系：

　　乙工效=三人工效和-（甲+乙）的工效…………①

　　乙工效×工时=工作总量…………………………②

　　然后，通过巧用“单位1”，还可找到更好的办法：

　　设乙独做，x天可以完成。若把整个工程看作“单位1”，那么乙每天

　

　　

　

　

　　

　　所以，其解答就比较简便、快速而巧妙了：

　　设乙单独做，x天可以完成，则有

　　

　　

　　即乙独做30天可以完成。（答略）

【巧用直觉思维】 有些题目的条件和结构比较特殊，常常不需要把全部条件用于计算解题，而只要根据其特殊性，经过一次或两次计算，就能将题目解答出来。这是“巧用直觉思维”的解法。例如

　　“从同一个地点步行到火车站，甲要40分钟，乙要30分钟。甲比乙先走5分钟，乙出发后，要走多少分钟才能追上甲？”

　　

　

　　

　　若巧用直觉思维解答，可以这样去思考、解答：

　　甲先走5分钟，他比乙会晚到火车站5分钟。那么，追及时，应是乙在路程的中心点追上，故可直接用30÷2=15（分钟），求得题目的答案。（答略）

　　又如，“工厂运来一批煤，计划每天烧3吨，可以烧12天。实际上每天比原计划节约0.6吨，实际上比原计划可多烧多少天？”

　　巧用直觉思维，可以这样思考：实际每天节约煤0.6吨，相当于实际每

　

　　

　　再如，“有一只底面半径为30厘米的圆柱形水桶，桶中有一段半径为10厘米的圆柱形钢材浸没在水中。当钢材从水桶中取出时，桶里的水下降了5厘米。这段钢材有多长？”

　　按一般方法解，必须先求钢材的体积（即下降的水的体积），再求钢材底面积，然后求钢材的长。这是很麻烦、很费时的。若用直觉思维思考、解答，可以设想一下钢材底面积同水面积的关系，再找出钢材长与水面下降部分的关系，便可不用求积，而直接求出钢材的长度：

　　根据水面半径30厘米和钢材底面半径10厘米，可知它们的关系是：钢

　

妙的解答方法：

　　5×9=45（厘米） （答略）

【巧妙放缩】 有些应用题，由于条件和问题的特殊情况，从直接给出的已知条件中不容易找到简捷的解题途径。这时，我们不妨把某一个已知条件扩大或缩小一定的倍数，促使其他条件相应地发生变化，由此往往能找到简单的解法。例如

　　“5千克大米的价钱相当于0.8千克食油的价钱，如果2元钱可买2.5千克大米，那么8元钱可买多少千克食油？”

　　按一般方法解答，需要先求出5千克大米的价钱是多少，再求出0.8千克食油的价钱，然后求出每千克食油的价钱，进而才可求出8元钱可买的食油的数量。

　　若采用“放缩方法”，可把其中一个条件放大几倍来思考：将2元钱买2.5千克大米这一条件放大4倍，可知8元钱可买10千克大米。因为5千克大米的价钱相当于0.8千克食油的价钱，所以，10千克大米的价钱可买食油0.8×2=1.6（千克），即8元钱可买食油1.6千克。（答略）

　　有些典型应用题，也可以用“放缩方法”去解答，从而较快、较巧妙地找出它的答案。例如

　　“鸡兔同笼，共头48个，共足114只。问：鸡兔各有多少只？”

　　如果把鸡和兔的足数缩小2倍，则鸡的足数和头数相等，兔的足数为头数的2倍。这时，鸡和兔的总足数与总头数（总只数）的差数，就是兔子的只数，故可这样解答：

　　114÷2-48=9（只）……………兔数

　　48-9=39（只）…………………鸡数 （答略）

　　上面两例，是单纯用放大，或单纯用缩小的办法解答的。但有些较复杂的应用题，就既要用“放大法”，又需用“缩小法”，才能使问题正确而快速地解答出来。

　　例如

　　“甲乙两个商店去年平均每月的利润，甲店比乙店多5万元。已知甲店

元？”

　　

　

　　　　

　　根据这一新条件解题，还难很快发现其数量关系，这时不妨把这个条件再缩小2倍，于是得到

　　

　　这样得到的新条件中，就可以清楚地看出，甲店比乙店每月多的5万元，也就是甲店比乙店多的那个

　　

　　于是，甲店每月的利润数便是

　　

　　乙店每月的利润数便是

　　6.25-5=1.25（万元） （答略）

　　还有比这更复杂一些的问题，可结合其他解法来运用“放缩方法”，使问题得到解答。例如下面的这道英国名题——“第三牧场的牛数问题（实际上也是个牛顿问题）”：

　　“有三个牧场，场上的牧草长得同样的茂盛和同样的快，它的面积分别

　　

　　二牧场饲养21头牛，可维持9个星期。假若第三牧场饲养的牛，在该场要维持18个星期，那么，这牧场应养牛多少头？”（注：草料是边吃边生长的。）

　　按照“牛顿问题”的解法来死套，是很难找到解法的。不过，当我们运用“放缩法”，假定三个牧场面积同样大，这一道在三个牧场牧牛群的复杂题目，就会变成在同一牧场牧牛群的简单题目了。这是因为题目中已交代：三牧场牧草同样的茂盛，并且长得同样的快。

　　

倍数），则

　　第一牧场可以有牛

　　

　　第二牧场可以有牛

　　21×（120÷10）=252（头）（仍是9个星期可以吃完）

　　那么，第三牧场是多少头牛18个星期可以吃完呢？

　　这一道用放大了的假定数据编成的题目，还可以改编成一道与它同解的应用题：

　　“有一个牧场，养牛432头，4个星期可以吃完全部草料。若养牛252头，则9个星期可以吃完全部草料。如果要在18个星期内吃完这牧场里的全部草料，那么，它应该养牛多少头呢？（草料是边吃边生长的）”

　　这是一道简单点的“牛顿问题”，可用“牛顿问题”的解法解答如下：

　　因为432头牛4星期吃的草料，等于432×4=1728（头牛一星期吃的草料）

　　252头牛9星期吃的草料，等于

　　252×9=2268（头牛一星期吃的草料）

　　而4星期吃完与9星期吃完，要相差

　　2268-1728=540（头牛一星期吃的草料）

　　显然，这多出的草料，是

　　9-4=5（个星期）

　　之内新长出的草料。所以，牧场一个星期长出的草料是

　　540÷5=108（头牛一星期吃的草料）

　　因此，这牧场最初有的草料是

　　（432-108）×4=1296（头牛吃一星期的草料）

　　现在，这1296头牛吃一星期的草料，要求能维持18个月，则能饲养的牛数就只能是

　　1296÷18=72（头）

　　但这牧场的草料是不断生长的，还必须用108头牛来吃掉每个星期新长出的草料，所以，能饲养的牛数总共是

　　72＋108=180（头）

　　不过，这还只是假定这牧场为120英亩所得的结果。实际上第三牧场面积只有24英亩，比假定数缩小了

　　120÷24=5（倍）

　　故第三牧场饲养的牛数，也应比这180头缩小5倍。于是可知，第三牧场饲养的牛数便是

　　180÷5=36（头） （答略）

　　这道题的解答，显然是得益于“放缩方法”，将复杂题转化为基本题以后，才找到其解答的。